the lambda of the world frequency

How did the medium of our world come about?

Here are terms used, where are explained in Oscilllation of the matrix

It is arbitrarily assumed that we exist and that the universe has a beginning. It is most likely not absolute. It is like the beginning of a day based on the past day. After the birth of the universe, everything else is no longer arbitrary but deterministic. In the beginning there will be a scenario like the Big Bang of (more less than more) accepted theory. The unimaginable forces, the extreme compression of space, immeasurable temperatures and a time dilation into the infinite let expect that only configurations of a states of highest harmony survived. In principle, the space itself found its most ideal configuration, such as:

1.Tightest packing of space-structure
2. A cycle of cascaded sub-cycles of time in (+) and (-) direction
3. The perfect balance of compression / decompression as space momenta

In this way the universe could present itself to the physicist as an empty space. No asymmetry of power, even light was integrated in the perfect harmony of this configuration. After the universe has start to expanded, the original configuration remained in the smallest cells, then the gaps caused by the expansion were filled with a new degree of freedoms (according to Feynman). They became filled with heat, light and motion. The rest of the course is known to us. However, one event has not yet been mentioned: the collapse of the rod resistances (the color distances or lambda) in the order of S1; S3; S9 (scales), which created the fermions as an oscillation with vector to the 4th spatial dimension.

More info in http://matrix-4 scale 1

The Dynamic of the Matrix

The term MATRIX is a spatial network that consists of tetrahedral with internal distances in the form of octahedral, is scalable, allows time to act in two directions and has elasticity. Since it is assumed that physicists also read with us, it should be noted that Euclidean space is generally used. However, this is not isotropic and is used in the sense in the scale of its units or their rod lengths (color-distances). The same applies to the size of the proton (in the area of its collapse), in the area of other fields with the units of the respective scale and in the area of the EM space with the units of charge. The spatial network of the matrix is the basic structure in all areas, but its effect becomes less and less important at larger scales and ends at the well-known analog quantities where, depending on the experiment, relativistic space can be used.
Now some terms have already been used here, which are explained in more detail in the Page MATRIX
 

The tetrahedron structure is explained in MATRIX Teil 1 In the sense of an equilibrium, only the tetrahedral are importand. The octahedral are just gaps between them. In terms of collapsing rod lengths, however, only the octahedral are considered, since it is their diagonals that collapse. In physics they are interpretated as quarks.

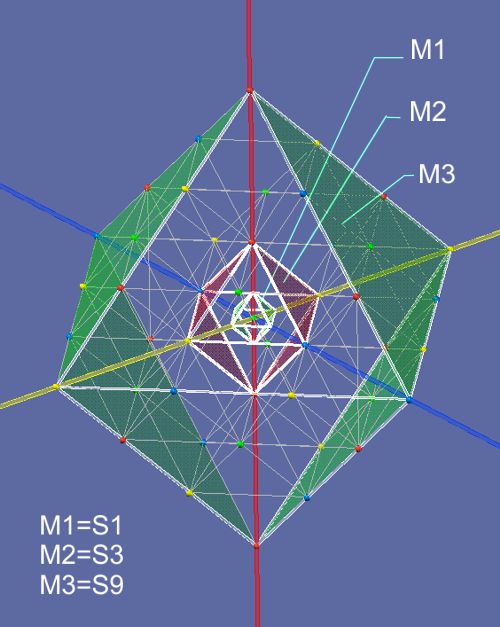
The size of space depends on the choice of its units. Apart from the 1 to1 representation of rod lengths, the unit of a S1-octahedron is considered as an proton. The field areas around the proton are dependent on the scales S1; S3; S9 etc., which are in a 3^x / 3^(x+1) relationship to each other and are based on the structure of the superimposed octahedral; more in collaps to Black Hole

The equilibrium in the tetrahedron area basically does not emit any forces, the space is therefore called empty in the sense of normal experiments. In this sense, space can also be considered as isotropic. This assumption provides correct results for the explanation of the charge fields up to the material properties of matter.

The quantum structure remains in all size ranges. Basically, it shows effect in all scales, but is heavily overlaid by the analogues distribution effect in sense of 1/r^2. However, the scales can also take on any size up to astronomical ranges, making quantum effects theoretically there possible in all scales.

A quant is the momentum of h from pulses and length. Since the momentum h is invariable, the length is variable. This means that quantum quantities cannot be used as units of any order of magnitude. The quantities are related to each other in the ratio 3^x / 3^(x+1), ; S1; S3; S9; etc. and are fixed sizes of space units and apply to the subatomic range. This also automatically defines the pulse size of its scale.

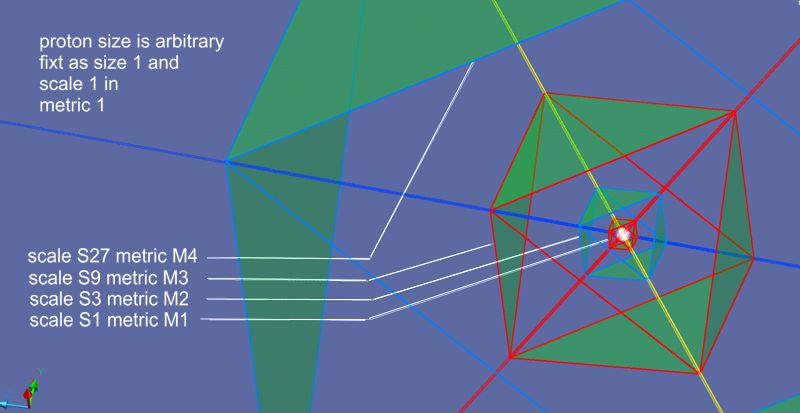
The picture above shows the different units of different scales. The momentum emitted into 3D space by oscillation of a proton has a geometric size S1 and is derived from E=h·c/ʎ to E=p·ʎ. This means that the momentum p·ʎ = 1 moment or a quantum with almost infinitely small ʎ. Without the consideration of the Matrix it would be a photon surrounding the proton. See also the Compton wavelength ʎ=h/m c. All other fields around the proton primary field are secondary fields, each with 1 quantum difference in the geometric quantity S3; S9; S27 etc.
Pulse p here is not mc^2 (here p=h/ʎ) and should not be confused with the energies of this oscillation with vector into the 4th space dimension (mass). It is just the side effect of this 4D-oscillation in normal 3D space, which has the geometric structure of the Matrix of tetrahedral and octahedral. It seems, that the fermion-oscillations with vector to the 4D coordinate effects a communication frame in 3D space. The rest energy (mass) of a proton E=mc^2 remains in the primary field S1 and only propagates indirectly in 1 quantum steps into the secondary fields. If that weren't the case, then charge would be 511´000 eV (mass of an electron) instead of one quant or1 eV.

The hierarchy of fields

One can also speak of the hierarchy of standing waves.

First the term Matrix in connection with field and waves:
The term Matrix consists of space-time and pulse, whereby pulse also means energy depending on its effective distance (p=h/ʎ). In QT (quantum theory) the quantities or portions of space, time and pulse are placed in a defined relationship. Every space no longer consists of x,y,z but of the unit of space, a portion (quant), which is also space and stands in certain harmonious relationships to the higher and lower space cells. This portion is given a reference value to the space of the smallest field around the proton e.g. the field with the size of the scale S1. With the defined spatial portions, time and pulses are also defined according to the QT.
→ Time t=ʎ/c where c=speed of light and ʎ=radius of the field size.
→ ʎ=h/Pulse or h·c/E, where E is an energy.
Every space size therefore has its own ʎ (wavelength), its own time and its own pulse. The hierarchy of space sizes therefore also results in a hierarchy of time and pulse sizes.
The matrix is therefore not just a spatial structure, but a harmonious interaction of space, time and pulses on the respective scale. In principle, it is always the same or integer distances that lead to the geometry of Matrix.

How to represent the geometry of the Matrix structure

I have to reminde that the Matrix as a medium of the universe and its fabrics consists of tetrahedral, which in their volume-filling results in a pattern of gaps by the shapes of octahedral. This results in an image that the Matrix can be seen as a seamless space filling by octahedral or by tetrahedral. The impact of the 4th spatial dimension force us to see tetrahedral as carriers of spatial points of power, which as equilibrium result to zero as a sum. The octahedral thus become the gaps in this space and the weakest point of the structure. In case of deforming they become by a certain status values of (++; +-; -+ or - -) by the collapse of its structure. If 3D space would be seen as a 2D surface, the collapsing 3D space into 4D direction (as tensor) or into the "n" coordinate of 4D space (x: y: z: n) causes a bending of 3D-surface.
Now we have to assigne the criteria time and pulse or the momenta h to this structure. First, the 4 status values ​​(++) (+-) (-+) (- -) are assigned to the center of an octahedron.
The first rules emerge:

• In sense of an equilibrium, no color should be the same as its adjacent colors.
• In sense of spreading the energy, colors of adjacent fields should be the same in a line

The geometry of the Matrix does solve this in that way:
If space is filled with tetrahedral by side length S1 (arbitrary assumption), then this lambda or rod length S1 results in a perfect equilibrium. There, no color has the same color as adjacent colors.

If the side length S2 is used in the same structure, the same space status-color is always found for each space point. The space becomes conductive for all disturbances caused by energy-differences. This shows us what effect the distance between the points will have. This will be discussed in detail in Matrix Part 1

When explaining subatomic processes, the momentum h must now be introduced into the matrix structure as a universal constant. The components in this solution are the harmonic relationships of the individual frequencies. The term frequency was therefore already explained in the previous article and the link  Oscillation . Each point in space or each color is an oscillation that is in a certain harmonic rhythm with adjacent colors. The resonance here is C-G-G´ or C-C´ in the sense of 12-tone music. This gives the aspect ratios of (-) to (+) e.g.

 <  <  <  3^-4 ; 3^-3 ; 3^-2 ; 3^-1 ; 3^0 ; 3^1 ; 3^2 ; 3^3 ; 3^4 > >  >

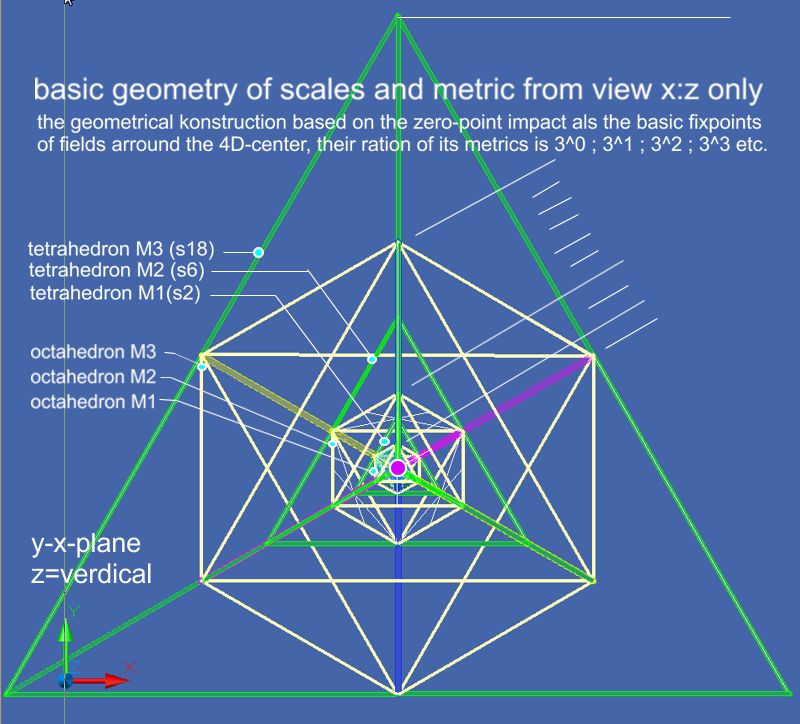
To explain particles and their cascaded fields in different scales, a look at the geometry of Matrix will become nessasary.

The picture shows the octahedral in white, the tetrahedral in green. The center in the geometric bodies is exactly at the same point in space. While the geometrically identical shapes are nested in each other, the octahedral of the same scale are touched by the tetrahedral of the smaller metric. The 3 diagonals of the octahedral are clearly visible with their 3 colors, here magenta-yellow-blue, which run unaltered and through each scale into the next higher one. It is recognized that all tetrahedral have the 4th color, here green. This only applies if the tetrahedral represent the maximum extent of a scale unit like S2: S4: S6 etc. That is an important point: While the white octahedral represent a standing wave, the green tetrahedral are the pulse transmitting space.

How it comes to 4 dimensional waves?

As described in the chapter Matrix / Oscillation, the 3D space can be imagined as a surface with its vertical as a coordinate to the 4D space. At the coordinates x; y; z, z whould be suppressed and replaced with "n" as a vector for 4D space. Since 3D space is now a spatial structure, for practical reasons the surface can be thought of a thin fabric, the network of which, like a knitted mesh of threads. Each stitch is a tetrahedron with 4 vertices (4 colors).

Thus the symbolic surface of space becomes now partially real. It gets a top and bottom. In our thought model, under certain circumstances, this surface can become bends in the shape of waves. In this sense, the bends have an upper surface where the wave cress creates tensile stress and at the same time at lower surface, the bends generates compressive stress. That's exactly what happens in reality. The phenomena on the top generate the equivalent values on the bottom, a scenario of supersymmetry is shown here.

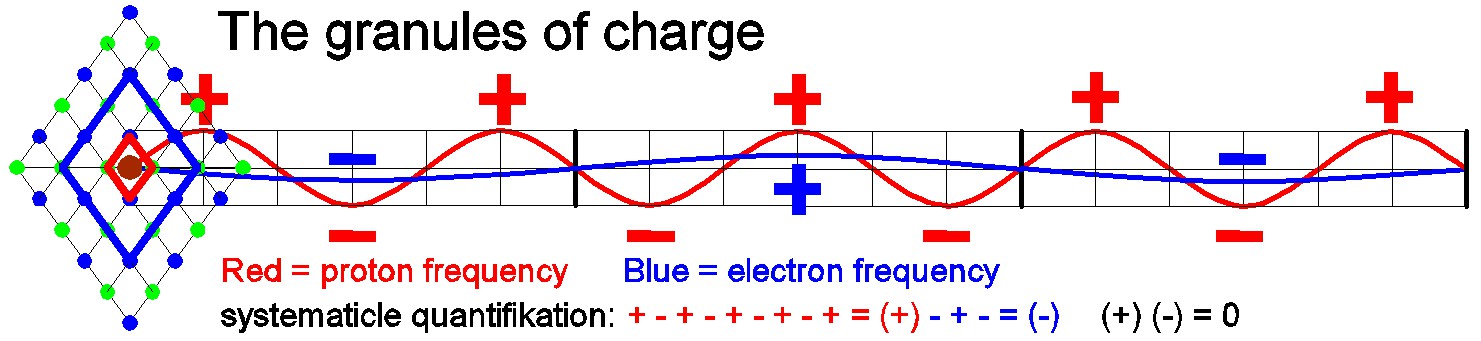
The picture shows on the left the space sizes S1 and S3 with parities (+) and (-). In this example here is a proton inside of a positron, i.e. representing a neutron. It symbolizes the ratio of waves: blue as S3 and red as S1 in a ratio of 3 to 1.

Space becomes properties and these become space

With the assumption of a 4th spatial dimension, properties of 3D space can without it only be assigned to the particles and fields as arbitrary attributes. Here, with including the 4. dimension they can be explained. The 4th spatial dimension has a local impact on 3D space. Local fields (as standing waves) can be explained in this way, even if the medium of space would normally carry away any influence with V=c. That's what the medium does, but in this case (4D) we can't see it. The quantized time propagates in 4D direction. The first field (S1) in 3D space, the primary field of the fermion, is indirectly generated only in 3D space.

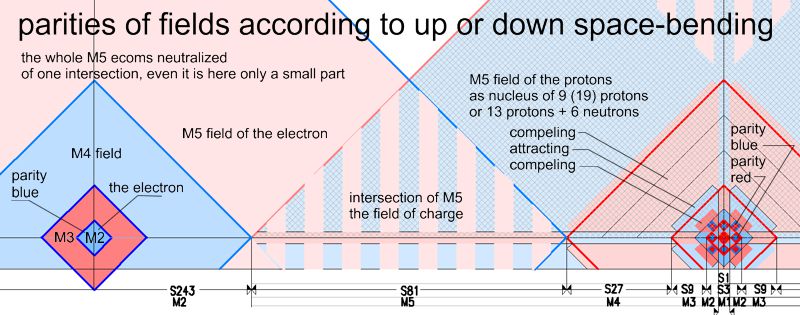
The picture shows the influence of the field parities of an atomic nucleus (atomic number 19) and an electron on the S orbit or K shell. The expression "parity" is used here instead of "charge". That makes sense, since it is, as described in Matrix-charge, the bending of the 3D space what causes the attraction / repulsion effect. However, this bending is not static but oscillating. A straight space cannot oscillate, but bending requires an oscillation.The oscillation, however, can have no charge. It is (+) and (-) . Since all spatial distances correlate harmoniously and have their own time and pulse, all oscillations are also harmonious with one another. I.e. if two fields have the same parity, they repel each other, if they have a different parity, they attract each other.
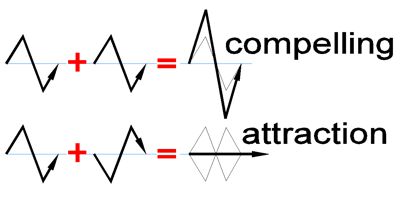With the hierarchy of space and its field sizes the problem of V=c was also solved, since the hierarchies of  harmoniously nested space sizes have an interaction of the same or different parity and are therefore independent of time. This means that in large distances large fields (S81 etc.) are in effect and in small distances small fields (S3; etc.). Time only exists for objects outside the oscillation.

 What exactly does it mean?

All interactions happen as if they are simultaneous. Through the own metric of space sizes S1; S3; S9; etc. there is no more time effect, only parities. If e.g. a particle P1 (x1; y1; z1) 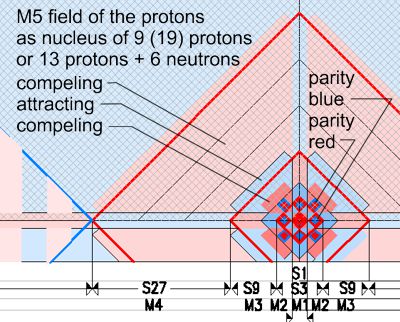 interacts with particle P2 (x2; y2; z2), P1 has the parity (+) and P2 the parity (-) then it doesn't matter where their fields are intersect. P1 can only interact with the S9 of P2 with its own S9 field. The fields, regardless where, always interact with (+) or (-) and in this case are attracted. They change their values ​​in pica seconds from (+) to (-), their parity always changes with the location, so they are always attracted, regardless of their oscillation status. Interacting always means a field overlay of the same field size e.g. P1 by S27 and P2 by S27. Again in plain text: the rhythm and oscillation of this kind of field (here the field of charge) is the same in the whole universe. Although time delay by V=c is built in, it has no influence on status relation or their parities, since particle oscillation does NOT has any motion, but only propagates and is always as a local event. The connected properties such as charge are thus independent of V=c and act as a permanent effect. That is the main reason, why to day's physics think of charge as a permanent property.

Fields of fermions

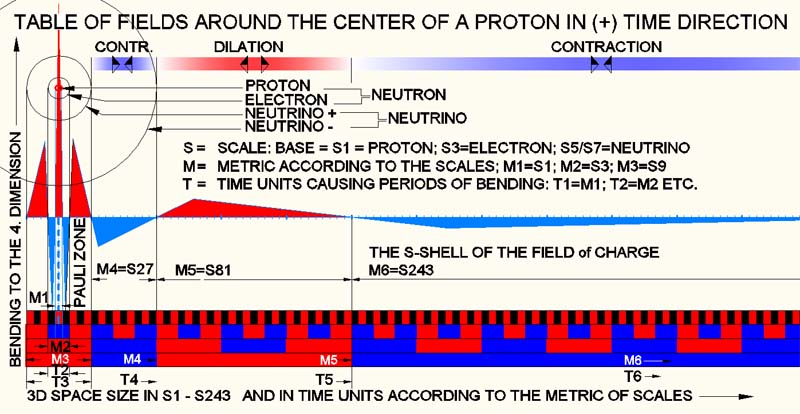
The bending of 3D-space effects first S1. S1 correlates with the frequency corresponding to the 4D-impact (the 4D oscillation) (F = h/p). In short: a balance is formed already at the birth of the universe (or when the proton is created). After that, no energy flows. Any asymmetry would have dissolved already at the birth of the universe. Only a perfect system of a equilibrium whose values ​​add up to zero would have survived. In the case of a proton, this means (according to experiments) a lifetime of 10^27 years, longer than the age of the universe ?!? The space sizes S1; S3: S5 and S7 etc. are basically empty quanta, which can be filled "without penalty" or without causing a flow of energies. The picture above shows the cascades of the fields around a proton. These fields are not only fields of activity in the 3D area, but also bends (as indicated schematically by triangles) from the 4D-perspective. As described in the link in Matrix: Oscillation. They cause the bending (compression / decompression areas) in 3D-space. It is the elasticity of the Matrix as a medium that seeks balance in combinations of such (+) (-) areas. It causes the effect of attraction or repulsion instead of a permanent property (+) / (-). The (electrical) charge is now explained as an parity, a quantum domain instead of being arbitrarily determined for purely mathematical reasons.

Hyper fields

The question arises as to how a distant electron finds its way to the right place in the field region of the atomic shell. Is this all chaotic temperature and coincidence?

We now know that an electron is pulled by its antiparity to the atomic shell. It is a phenomenon caused by the property of space to compensate for disturbances in the matrix structure, which is here considered attraction in physics. So how does the matrix structure work as a medium of attraction?

These are the secondary fields as hyperfields around the fermion, here the electron. These hyperfields group themselves around the primary field like babushka dolls. In our case it is the ʎ (diameter of the field) of the charge field, also known in physics as an orbital. Even in so-called "empty" space, an electron interacts with the proton with its hyperfield. There is no "spuky effect at distance" (Einstein) but rather the interaction of a hyperfield of the proton, e.g. S59049 (S3^10) with the same hyperfield of the electron. The parity of the electron always has a counter-oscillation to the parity of the proton field. The very small force of this interaction causes the electron to find its way to the place in the electron shell. A deeper insight you find in the electron

Hyperfields of photons but also of electrons or protons are the cause of effects even at the analogue size of an experiment (i.e. outside the quantum size). They are the cause of interference fringes in the 2-slit experiment or Bell's theorem. They are the cause of chemical reactions, magnetic forces and ultimately the states of matter. Theoretically, metaphysical phenomena can also be explained with this. Magic only exists outside of the matrix theory. Further consequences of a philosophical consideration of the matrix of the medium of our universe can be found in my other papers:

The MATRIX of all what is
The vibration of the world-medium
The geometry of the medium space
The universe
Friedmann-space and the space-matrix
The space-time continuum
The space- and time-illusion
Particle in the matrix structure
The Electron

At Christmas 2016 I started the project to put my idea of the matrix of an world-medium on the web. In 2017 and 2018 the ideas in my head and my 3D CAD platform grew into a zoo of solutions that required a logical order. In July 2018 I started to document these ideas in my page MATRIX. The individual topics actually produced themselves and stunned me with their surprising solutions.

Gunter Michaelis, Griesbach in Switzerland, the 21.10.2023