Particles are epiphenomena arising from fields. Thus the Schrödinger field is a space-filling physical field whose value at any spatial point is the probability amplitude for an interaction to occur at that point. Elizabeth A. Hobson
A field in the context of the matrix is a vector and tensor oscillation in a 4-dimensional space whose density and energy depends on λ of its oscillation. With the quantization of λ, space, time and its energy also become quanta. Therefore, not every (or any) point is seen in the matrix, but only matrix points.
In part 4, the "particles" quarks, protons, neutrons, electrons, neutrinos with all their antiparticles are to be described in terms of space, time and force geometry. They should be explained from a stable basic state of the matrix. The prerequisites, the paradigms were described in parts 1-3. Briefly addressed here:
The dimension zero of value 0 becoms a value in its multiplication
(existence).
The resulting 3 spatial dimensions form our conscious space.
All masses and inertia are result of the 4th spatial dimension.
Time is always the influence of the
next higher dimension.
The cause is c, the limitation of simultaneity.
Our vision is always in (+) time.
This results from a 4D oscillation with V=c
A 4D oscillation V<c would allow therefore a (-) and a (+) time.
The super symmetry (SUSY) shows both views, (+) and (-) time.
The (-) time makes the full cycle (spin 1) to an equilibrium
A particle here is no longer a separate field, it is the state of the medium at that location
From this point of view, no new particles are created in CERN, only the state of space in this location changes. All forces, all interactions, arise from the disturbances of the original oscillation of space, time (it too oscillates) and pulse.
A standing wave is a oscillation with vector (as tensor) into the 4th dimension..
What does modern particle physics say:
Traruh Synred, Ph.D. in
Particle Physics means :Like all wave function they only predicts the
probability of ‘finding’ the particle in a place. ‘Particles’ exist all the
places where their wave function is non-zero. A ‘particle’ is a
excitation/wave that exist in many places. The weird point is how something
that is spread out is detected in only one ‘spot’. The probability of
‘finding’ them or other detectable occurrences is give by the Born rule ..
(The value of the absolute value of the wave function squared). Though
called ‘particles’ for historical reasons they are not like tiny marbles.
What is considered empty space is only the manifestation of unawakened matter Nikola Tesla
A deep look at the medium from which particles are made
The tetrahedron-octahedron structure of the matrix allows 2 different spatial structures that become visible depending on the viewing angle. The tetrahedron space has a 60° structure and the octahedron space has a 90° structure. It's the same spatial structure. Depending on which tetrahedron or octahedron is marked, the structure becomes tetrahedra with gaps in the shape of octahedra or octahedra with gaps in the shape of tetrahedra. Both perspectives are called here MATRIX.
With these paradigms all forces, charges and particles as well as the
photons should be described. This description shows a basic solution without
quantification. The methods of measurement in Coulomb or Newton are not used,
the Planck quantum of action h is used as the
basic unit.
h=E·ʎ/c as a momento with always the same value.
The Matrix Field Theory MFT as a theory of new paradigms shows the physical background in the following.
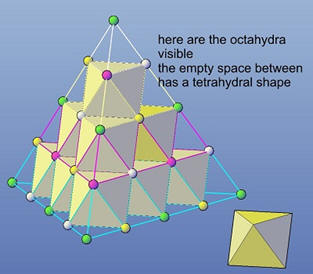 The edges of this
structures are connecting lines between fields, shown here as 4 colored
spheres. The 4 colors are the states (++)
(+-) (-+)
(- -), which result in an equilibrium in
space-time and pulses in the matrix. The nature of equilibrium theoretically
allows any density, strength, and magnitude of energy without affecting
adjacent spaces. It can bear any scaling, whereby the distances can
theoretically be of any size, including Planck's length (1.616·10^−32 mm).
With this, energies of e=h/ʎ =~1.5·10^15 MeV are recorded. The
meaning of these numbers is difficult to grasp, since everything is
unimaginably small and can only be grasped theoretically. One has to keep in
mind that everything oscillates and the colors change on the scale of the
Planck length Lᵨ within Lᵨ/c or ~3·10^-33 sec. For this reason we work here
with the scale S1 of the matrix (the size of protons) and the invariable Planck efficiency
h.
The edges of this
structures are connecting lines between fields, shown here as 4 colored
spheres. The 4 colors are the states (++)
(+-) (-+)
(- -), which result in an equilibrium in
space-time and pulses in the matrix. The nature of equilibrium theoretically
allows any density, strength, and magnitude of energy without affecting
adjacent spaces. It can bear any scaling, whereby the distances can
theoretically be of any size, including Planck's length (1.616·10^−32 mm).
With this, energies of e=h/ʎ =~1.5·10^15 MeV are recorded. The
meaning of these numbers is difficult to grasp, since everything is
unimaginably small and can only be grasped theoretically. One has to keep in
mind that everything oscillates and the colors change on the scale of the
Planck length Lᵨ within Lᵨ/c or ~3·10^-33 sec. For this reason we work here
with the scale S1 of the matrix (the size of protons) and the invariable Planck efficiency
h.
The basic medium is at field scale 1
If pulse and distance are variable and h is invariable then Pulse becomes infinite at distance 0. Clearly this makes no sense. A smallest size is required, which can serve as a reference for further considerations. The Standard Model (SM) uses the Planck units length = 1.6 10-25 m, mass = 2.2 10-8 kg and time = 5.4 10-44 s. Since these values still use the reference of our normal world (m, kg, s), they make no sense here, since they are too strongly distorted by the theory of relativity or the Lorentz factor in the considered order of magnitude. Space in the scale of (m, kg, s) seems to be still isotropic but will be quantized in the scale of protons.
Here, the geometric references should first be shown as a basis for understanding, after then to include the relativistic distortion as a separate task. It therefore made sense to me to take the field size of a proton as the matrix scale S1 to explain the geometric relationships of other fields as S2, S3, S4 etc.
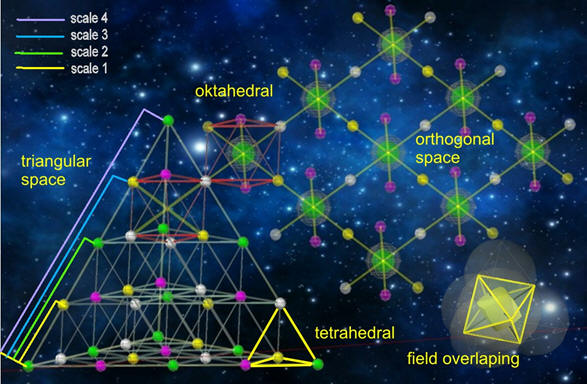
The upper image clearly demonstrates the view of triangular and orthogonal space. It's the same spatial structure. Here stages of space are related as colored spheres, the diagonals of equal colors are shown, which I call here the highway of energies. These are the way out of energies in a dense structur of mass carrying particle. It also shows here (red) an octahedron separated, which when put together, would again form an orthogonal structure. All of these are views of the same spatial structure.
Geometric relationships of dimensional representations
Knowing a dimension is understanding its geometry. As the first axiom, a size must be assigned to the dimension D0. Only then does it exist (look Dimensions) Only then can the conditions of dimension D1 be met. Only then can any number of dimensions manifest as degrees of knowledge. The matrix theory gives us the rules of an exact consideration.
1.) Equal bar lengths on a scale, or its collapse in shorter lengths with the ratio 1/3. This does not violate the equilibrium conditions of the matrix.
2.) Everything oscillates. Here, too, the measure is frequency. Space, time and energy therefore oscillate. The sum of all the conditions of one oscillation is always zero.
3.) All considerations only apply to stable states. The rod lengths (λ) and their frequencies are in the ratio 1/3^x (1-3-9-27-81 etc.).
4.) These conditions go through all dimensions. The collapse into another dimension is reflected in a new multidimensional harmony or stability.
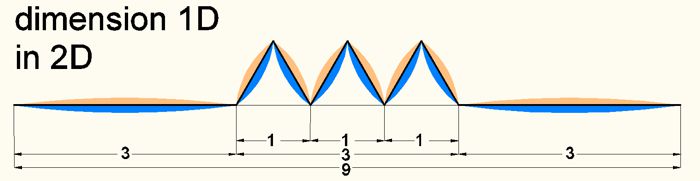
Example 1: The bar length 3 is compressed to bar length 1. As a graphic in D2, it is possible to show the shortening from S9 to S3 in such a way that bending up into the new dimension D2 can have stable rod lengths (S1) again. It must be realized that from D1 this bending appears as an imaginary value (tensor). This tensor presents here the bending H1=√(1^2– 0.5^2) = 0.866

Example
2: Only the compressed part is shown here (white structure in D2). The
representation in D3 allows to show the bending up to the next higher
dimension. At the same time, the deflection height can be shown by
color yellow or green as a vector of imaginary deflection to
compression or decompression, when the vertical is the indicator of pressure/depression. The white structure would then be the
statically acting zero value of space.
The result is the bending
heights H2=√(H1^2 – (0.5·H1)^2) = 0.7806.. H1 would be the imaginary value in D1
and H2 the imaginary value (tensor) in D2.

Example 3: The octahedrons with the bar lengths in white show the compressed in D3. The octahedron consists of only 3 colors. It is the space between 8 tetrahedrons, which but consists of 4 colors. One has to imagine space D3 as a network of tetrahedrons, where the octahedrons are the gaps. Nevertheless, the process of energy balancing takes place in octahedrons. The missing 4th color of the 3 octahedron colors get formed in their center as an energy balance. This is shown here as balls in green and yellow. In them, the collapse into the D4 dimension takes place as compensation. Since an isometry on a D2 surface has no way of representing the vector in D4, the D4 vectors (tensor) remain imaginary.
In the image an attempt is made to show the vectors perpendicular to the
surface made by diagonals toward D4. The value of bending up here would be
H3=√(H2^2 – (0.5·H2)^2) = 0.6760.
H2 would be an imaginary value D2 to D3. H3
would be an imaginary value (tensor) D3 to D4.
In each dimension imaginary tensors of the next higher dimension are possible.
Collapse of the rod force and bending up into the 4th spatial dimension
In every scale there is an equilibrium of 4 states, nevertheless disturbances from the environment are introduced into the equilibrium systems of tetrahedra and octahedra. The system (e.g. octahedron) changes its state accordingly. It transmits these disturbances back into the environment until an entropy is reached. During this process, a resulting moment arises in the center of octahedra, the manko color. As shown in scale, the even-numbered scales are S2; S4; S6 etc. not able to pick up forces of distortions. They transmit them with V=c into the surrounding space of the matrix. In center of the affected octahedron, however, the culminating forces of compression (the diagonals) can lead to a punctiform inflection into the 4th spatial dimension. Well, when exactly does this happen?
The experiments at CERN show that kinetic energy converts to mass. New particles are created. The same process is assumed at the center of galaxies. The BB theory assumes a reverse process; from a hyper-density, energies are emitted as mass, the birth of fermions.
 The
matrix theory assumes that the input of 4D radiation with V=c perpendicular
to the 3D space oscillations creates the phenomenon of particle. Strictly
speaking it is a double oscillation, the warped space oscillation of 4D
tensors and the 3D vector oscillation of particle fields
(as space compression and depression). They are the 4 states that summed up
to an
equilibrium at the corners of a tetrahedron.
The
matrix theory assumes that the input of 4D radiation with V=c perpendicular
to the 3D space oscillations creates the phenomenon of particle. Strictly
speaking it is a double oscillation, the warped space oscillation of 4D
tensors and the 3D vector oscillation of particle fields
(as space compression and depression). They are the 4 states that summed up
to an
equilibrium at the corners of a tetrahedron.
Since the fluctuation as tensor values in the 3D locality can at least not have a direct energetic influence on the 3D space (rectangular vector), it acts there as a time pulse, the effect of which can only be explained in the alternation of local simultaneities. But yes, even Stephen Hawking was at a loss there.
How can the collapse of diagonal forces of octahedra into the 4th dimension be imagined?
The rod force phenomenon arises from 2 properties:
1. Resistance or Elasticity of Bar Medium (W=δ*L)
2. The buckling
force (KK), a moment p=hc/ʎ=1 quant
While W is the resistance of the medium, the energy of a single rod is
contra-proportional to the rod length d (p=hc/ʎ). Thus, the scale can be seen
as vertical and the resistance as horizontal in a diagram. W would there be
seen as a horizontal parallel to S(x), while KK gives a progressive curve
due to the geometry of the matrix. The 2 curves will inevitably intersect
where a bending of the bar force into the D4 is to be expected.
The list
shows the old Standard Model (SM) values with the new values. The new values
are the conversion of the values of the SPIN theory to values of
oscillations. The values of the old idea of super-symmetry (SUSI) become
parities of (+) and (-) time. The collapse as a bending up into the 4th
spatial dimension establishes the phenomenon of mass and inertia.
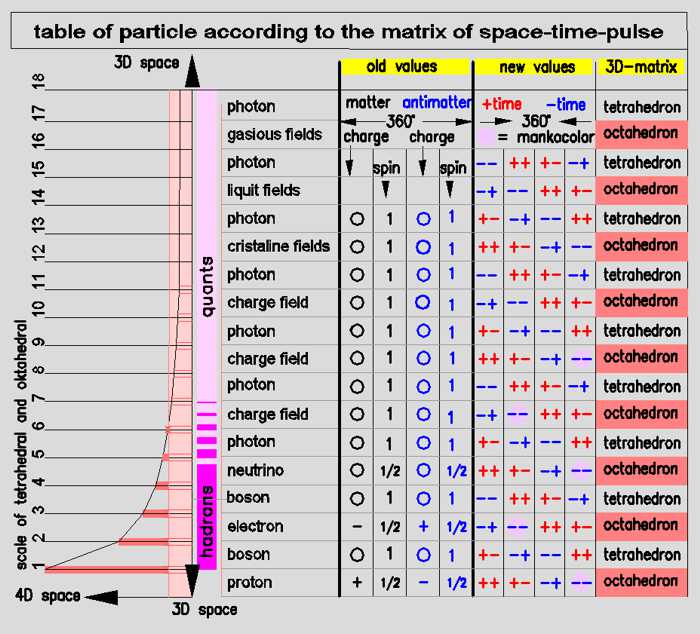
A prima Vista, the quarks are missed. Spin and charge are eliminated. All particle properties became states of one and the same space. The purple values are those of the deficiency color and thus tensor values from the 4th dimension. They are values interpreted as mass and inertia. All particle are now oscillations of the matrix.
The new List
1.) It shows the new values related to the matrix geometry.
2.) The new oscillation-parity-values replace the terms spin and charge.
3.) It shows
the old values of matter and antimatter (black and blue)
4.) It shows in
the new values (+) time and (-) time instead of matter and antimatter
5.)
No quarks are listed. This will be explained later separately.
6.) No
neutron is listed. This is explained in the Beta Decay paragraph.
The explaination of the list:
From left to right:
• The scales S1 to S18 (vertical)
• A vertically listed chart is
shown. Orange is there the bar resistance as a general property of space.
Bars are shown from S6. They symbolize the collapse in 4D. Since this is
dependent on the rod length (p=h/ʎ), this results in an exponential curve
that intersects with the level curve of resistance.
• The marking of hadrons to bosons
• The list of hadrons and bosons.
•
The old quantum values charge and spin
• The new values of the double
oscillation + - in (+) time and + - in (-) time.
• The assignment to the
matrix geometry
Matrix theory explains the new concept of charge: Charge
In this sense, the spin is also reinterpreted: Spin
The geometry of the matrix, its double oscillation, requires the incorporation of antimatter as an integral property of any matter or particle. SUSI
The front wave of radial expansion from the 4th spatial dimension (see nature of the universes) creates the simultaneity and cognition ability of our 3D universe. The reverse side of this front wave, an inside view of the expanding 4D sphere, is hyperspace. From this point of view every particle of matter is also antimatter.
Antimatter is the backside of matter and cannot be separated from it.
The fireworks of "Large Hadron Collider" reinterpreted
Let us remember Einstein's condition for space itself. Der Matrix Raum
“Nothing is more important than the fact that space isn't empty. He is the substance of the most powerful physical forces. " John Archibald Wheeler
The matrix theory does not accept any separation of fields or spaces, i.e. no completely detached parts of space with independent properties that are defined as quantum numbers in the SM (Standard Model). All properties defined as quantum numbers are actually local properties of the space which thus serves as the medium of oscillating moments. A particle in the matrix is therefore only the location, where its moments, its vibrational values, its state of relationship to the surrounding space entropy, its color value of the QCT etc. is recognized as particle. It is not separated from space, it is its local conditions.
A particle is the vibrational energy, the momentum of the disturbance of space or the balancing moment of the three moments of the octahedron, which encloses the particle as a spatial cell. This means that there is nothing other than energy that makes up our physical world.
A particle therefore does not find its way through space by pushing it aside; it propagates as a bundle of moments through the structure what forms the medium of space. The matrix consists of a structure in different scales, which forms a different resonance with respect to the basic frequency and therefore also has its own metric. The Planck constant h still applies here. This creates scale-dependent energy densities, i.e. rod lengths of the mesh, frequencies that are amplified or suppressed from the resonance to the base frequency, look at Scale of matrix . The relativistic changes in its values (Lorentz factor) are also quantized. This means here, the values within a scale and therefore within a frequency remain the same and have fixed values in its scale. However, the ratio of two such values (two measures) would have to be also an integer number.
The large picture shows that with the matrix space
structure and its integral values, local destruction in LHC can only produce
structural debris with integral values. As mentioned before, quarks can be
derived from the 3 diagonals of an octahedron, but gluons from the rod
lengths of the surrounding tetrahedron. However, the scales have different
energy values, which means that gluons are seen as carriers of different
energies (local space-conditions). However, things get even more complicated when e = h▪f is
applied consistently. Then it is the (mostly kinetic) energy of the
projectile that determines the rod length of the debris (λ=c/f -> λ=c▪h/e).
This is how particle generations of the SM arise. It is clear that the
chromodynamic values of QCD come from colors of the matrix (++
+ -
- - + -).
In the SM they are represented as ↑↑ ↑↓ ↓↑ ↓↓. Mathematically,
λ of quarks are valued as 1, but in the
matrix as 1/√2. This is because all values in the matrix are based on
scale S1 with rod length 1. The diagonals act with the ½ distance (1/√2 or
1/2•√2) to the center of the deficiency color. The distances between the
nodes of the octahedron in S1, however, have the size 1. The SM, however,
sets the reference to the quarks, which get the value 1 in their theorising
of QCD. This makes all the values of other rod lengths in the QCD 1/√2. It
is theoretically not wrong, but it is not practical. It is assumed in SM
that quarks form the basis of our material world. However, this is a dead
end of thinking. How can a basic element have a lifespan of only 10^-25
seconds and add to it, is approx. 200 times larger
(Compton wave length) than its container, the
proton. In other hand lifetime of a proton is about >10^50 times longer than
that of a quark !?.
The end of the story is that the matrix it self cannot be changed by any projectile energy, whatever size. The octahedron of a proton can be shot free of its specific moments, but never be destroyed. The energy of projectile also consists of a bundle of moments that hit the moments of the target with great severity and explode there star like into colorful fireworks, whereby all players in this game are moments where only get their intrinsic values from their position and relation to the matrix. We consider them as individual particles, their true nature but, the matrix, is recognized in the SM as emptiness.
It is the “empty” space of Einstein that replaces the ether and replace our apparent truth to become an illusion. Space is the medium and therefor can't have holes.
The Fermions
As described above, the fermions are the effective field centers of a 4D moment in 3D space. They do not really exist in 3D space, but they have an effect there. In principle, they cannot be moved directly by 3D-energies, but only by deforming the 3D space plane, which is subject to the limit V=c. Given that bosons are the 3D interaction between the fermions, they are bound to the interacting fields of fermions and are therefore limited in their range. Fermions are in that sense deformations of 3D space. It is the charge fields around these force centers, the primary and secondary field hierarchies, that are responsible for more complex structures.
Due to the historical tradition of discoveries made at different times, the Standard Model has a number of criteria that are difficult to correlate. These are listed here:
Spin --------------------------------- rotation 720° reduced to 360°,
hence 1/2 spin
Chirality, helicity ------------------rotation left-right
in 3D space (hand rule)
Antimatter --------------------------all quantum
values (including time) are reversed
Charge
------------------------------internal property of fermions
From this, Dirac was able to derive his spinors. All these values with
naive names now had a mathematical context. The matrix theory also derived
the 4 moments in 4D space as signs of the spatial density, (++) (+-) (-+) (-
-) or parities here as colors
(++) (+-)
(-+) (- -)
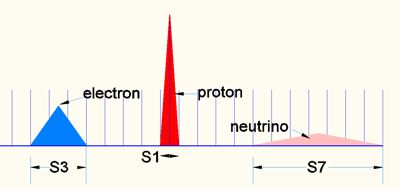 pix 8
pix 8
Here the 3 particles are derived from the SM (Standard Model). Vertically the 4D moment (E) and horizontally the relative field size in 3D. The values here are symbolic.
 pix 9
pix 9
It shows the proton (red) with the electron para field (blue) and the
neutrino para field (light red) in the matrix. Parafields are the logical
consequence of the matrix. Here they correspond to the formula λC =
h/(c · m0) of the Compton wavelength.
While in the SM the impact of the
particle was abruptly cut off from the neighboring space, its side effects
in the matrix space extend to the neutrino field. After the neutrino field,
the side effects of the impact are carried away in form of photons.
Therefore, for example, a proton (+) has a positron and an anti-neutrino
(see also β+ decay).
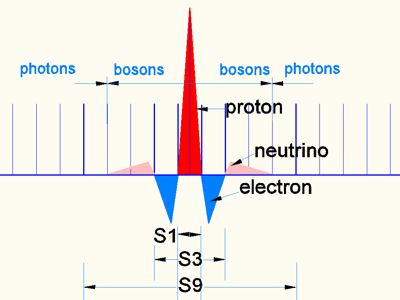
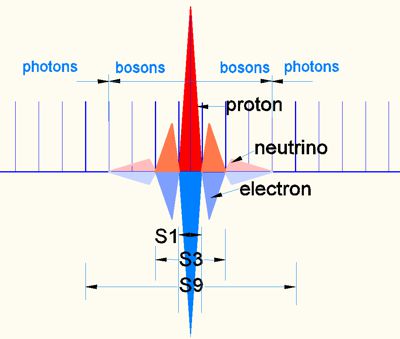 pix 10
pix 10
While Figure 9 symbolically shows only 1/2 cycle, the whole cycle (+ and - time) is shown here. These are the para fields of the double oscillation. All fields and para fields cancel each other out energetically. From S9 onwards, no more bosons can be formed and EM oscillations of the photons escape into the EM space.
The family relationships of fermions
In this paper, a symbolic graph is applied to explain the significant differences between the fermions. The rhombus symbolizes an octahedron. Its 3 diagonals (only 2 shown here) are symbolized by the arrows. The blue and green dots show the parity of the spatial cells in S1 (scale 1). Here it becomes clear that only one color was specified in the direction of the arrows. It is the diagonals that leak asymmetric energies into the V=c environment. They are the debris of LHC research known as quarks. The central point shows the moment in D4 that creates the phenomenon of mass. The lines show the octahedron that forms the primary field. Its color shows its parity with respect to the proton.
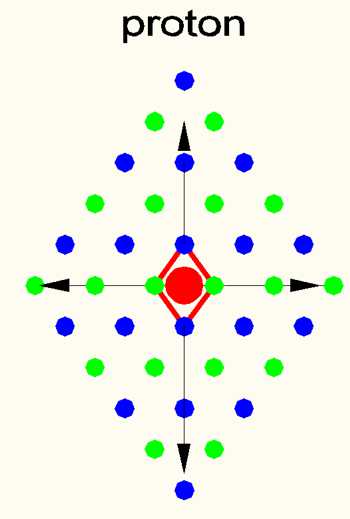
The protons are the primal race. They have the rod length of space size S1. S1 is the first size of the tetrahedron space, which can also be referred to as Unit 1 (U1), since they form the 1st unit size with 4 colors. According to particle physics research, there are other family relationships, but they are unstable and do not form complex structures. The philosophical basis of the matrix theory requires a harmonious relationship or resonance to the immediate environment. The condition is, that everything, the medium and its disturbances are in a balancing relationship which result in zero. It allows us to expect surrounding secondary fields as oscillations. These can only be expected in S3, S5: S7; S9 etc., since the geometric shapes (here as octahedrons) have the same center in this scale. Here it becomes clear that basically all fermions have the same geometric shape. They differ only in the depth of the moment to the 4th dimension. The resulting differences are therefore in the secondary fields, whose parity creates the actual difference. E.g. if S1=(+) then S3=(-) and S5=(+) etc.
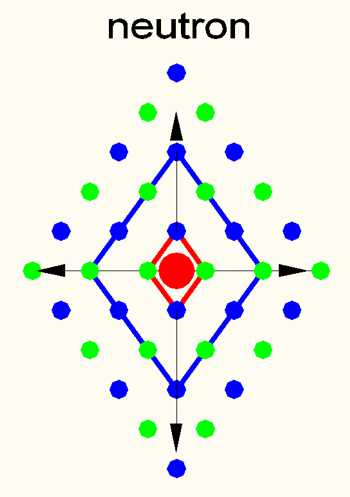
The neutron consists of 1 proton and one electron. The reason for this union lies in the secondary field of the proton. It is related to states of highest pressure during the birth of universe or to states inside of neutron stars while collapsing to supernova. The particles there are under such pressure that electrons are forced to concure the field S3 around the proton (S1). After the collaps in S3, the electron has the same center as the proton but on the (-) time parity of its oscillation. A neutron therefore gaine a balance in S3 and the subsequent charge fields S9-S27. In the Standard Model it is the reverse process of beta (+) decay. The corresponding Feynman diagrams suggest that the subsequent S5-S7 are also affected. Unfortunately, all Feynman diagrams assume that there are no protons and instead only show the 3 LHC debris as quarks, with only one quark mutating. It's the old classic notion that even the smallest particle can be shattered into even smaller particles. But particles are merely the disturbing energy of Matrix fields. Therefore, the higher the energy, the smaller the particle. It is nonsense that much larger quarks could use a proton as container.
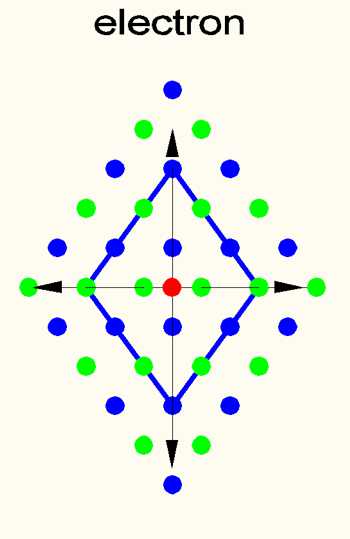
The electron is the little brother of the proton, it is exactly the same but packed in an octahedron of size S3. So it has three times the rod length as primary field environment of S1. This moment is the effect of an oscillation with the vector vertical to the 3D coordinates and has the opposite parity of the proton oscillation. Fused with a proton (i.e. it has the same center as the proton) it would cancel all subsequent fields. However, the normal state of an electron is its own separate entity. This interacts with the charge fields S9-S27 of the proton and is responsible for the effects of the periodic table. Theoretically, it also interacts with neutrinos S5 and S7. Theoretically, as S3 it also interacts with neutrinos S5 and S7. However, interaction energies there are already bosons and do not have any influence on "charge" S9 - S27.
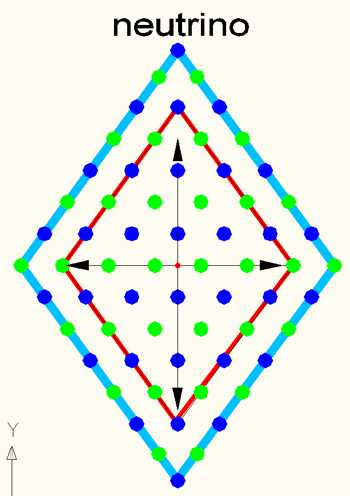
The neutrino is established above the electron in the octahedron levels S5 and S7, as symbolized by the red and blue lines. It is set as the limit between fermions and photons in the "table of particle" table. Like the neutron, it consists of 2 power centers that apparently alone as charge carriers in (+) and (-) time no longer have any effect on the 3D space. This will be the probable reason that made us only to discover 2 centers instead of 3. Perhaps experimental physics will one day be able to show us that the charged neutrino is a building block of aggregate states. That, it counts as a particle and not as boson is probably due to the fact that in S5 and S7 a minimal moment acts to the 4th dimension. The interaction of S5 and S7 (like the neutron S1 with S3) causes the subsequent fields S9-S27 to be neutralized, which means that the charge is eliminated. This is why it was so difficult to detect neutrinos in the first place.
This shows the symbolic references of the particles to the matrix geometry.
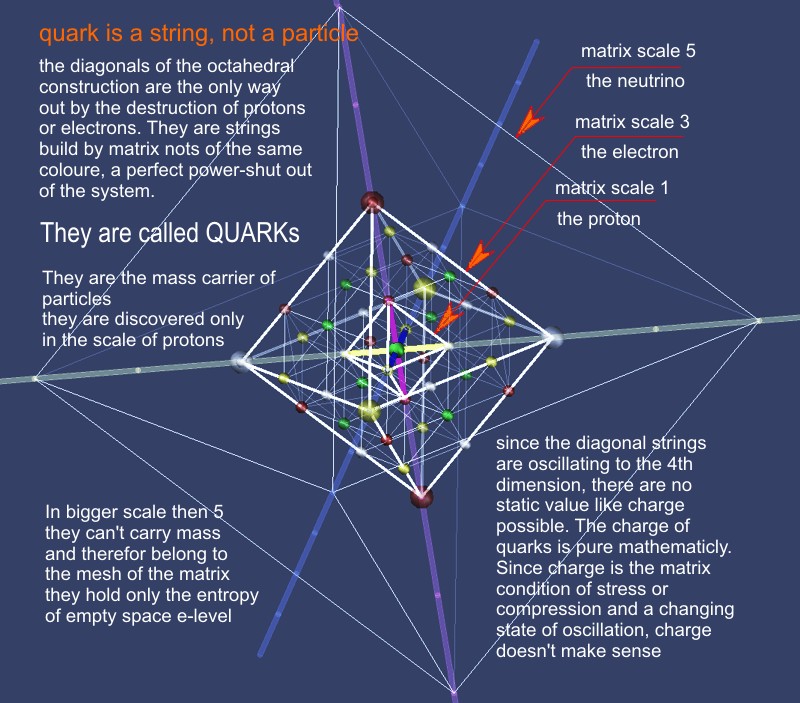
Quarks
In order to understand this chapter, the chapter "The fireworks of the LHC reinterpreted" should be read. -> LHC-firework and also "Matrix and the illusion of particle" -> particle illusion
In the matrix, it is the side lengths (λC = h/(c · m0)) that determine the density and energy in the octahedron of the particle (here in the S1 of the proton). In a collision at CERN, immeasurable energies hit the proton field (octahedron) deep into the lower scales (S3^-x). The elasticity of the matrix absorbs these kinetic energies and reflects them back to S1, whereby the temporary energies of the scale collapses escape into the environment (cloud chamber) along the 3 diagonals of the octahedron. It is the quantum nature of the matrix that releases these energies directly and not blurred (as 3 parities of the space oscillation). In the (measurement) environment outside of S9 (in S1-S9 they are bosons) they have the 4D moment (mass) of a particle with correlated S9-S27 momentum (charge). However, this only while the kinetic energy of the matrix mirroring is still effective (~10^-25 s). The parity of these 3 flashes of light (diagonals of the octahedron) can have one of these values (++) (+-) (-+) (- -). The chromodynamics of the quarks (Kuark tarts) should be redefined in terms of the 3 collapses of the scales S1, S-3 and S-9. Quarks are therefore bosons, sparks of brutal destruction. In CERN, therefore, no new particles are actually created, only new laureates.
The SM regards the quarks as the basis of our world. And that's only
because they were found during the smashing of the real building blocks of
our world, the protons. This created an unfinished image, which was firmly
nailed into the SM with the laureates chosen.
What's still wrong: Quarks
have a Compton wavelength that is about 200 times larger than that of
protons. Since a significant effect of the GR (Lorentz factor) has to be
taken into account in these areas of space, it can definitely be said that
quarks are larger than protons. How do they fit in? Quarks must be
incredibly intelligent to manage to always agree on one (+) charge in 10^-25
s. This is their lifespan. With this time, they guarantee the proton an
almost infinite lifetime. They are the chamelion of particles. Depending on
the energy level of the destructive input (usually kinetic energy), they
assume sizes of approx. 2 – 173,070 MeV. They have 6 different flavor
numbers and charge sizes with 3 as the divisor. You cannot collect or
isolate them. They are a spark of powerful destruction processes.
How do quarks look like in the matrix?
The matrix structure clearly shows that the 3 diagonals of the octahedron are responsible for the development of the deficiency color or the bending up into the 4D ordinate. In the extension of the diagonals, the matrix shows that only energy centers with the same color status (++), (+-), (-+) or (- -) lie on these diagonals. They are viewed as energy highways in matrix theory. The experiments in LHC will therefore constantly find debris as triplets with discrete energy values in 2 time parities, which were then defined as 3 quarks in 2 versions as UP or Down. Since these energy sparks are also part of an oscillation, the quarks were assigned spin ½. All just interpretation.
Since the matrix of space cannot be destroyed by its own disruption (i.e. energy), any energy impact, no matter how large, pushes the proton only down to a smaller scale and higher energy level. The compensation of this extreme tension creates W bosons and quarks. It is the latter who escape the low standards on the energy highways of the 3 diagonals. They don't get into S2 like normal bosons respectivly in S4; S6 etc. Their rod lengths relative to <S1 are d=0.5√2 =0.707 scale. They escape the high-energy scales only on the diagonals of the matrix. Their masses arise from the complex relationship of 1D energy impact to oscillation parity, to the 3D direction of the diagonals, and to the relativistic distortions of the energy/ʎ/time in 3D space.
Bosonen
The boson is a moment of resistance in the matrix, which, when deformed, restores the old state. It is the matrix that only allows quanta of a certain size E=hc/ʎ as an inner property, because ʎ is definated by its scale. Depending on the scale and size of the deformation, energies are released in quantum sizes to restore the balance. They are the "empty" octahedra S3-S7 and tetrahedra S2- S6 etc. The steepness of the curvature of space or the matrix in the scales S1 - S7 prevent these compensating quanta from breaking out. From S9 and as Quanta S8 and larger they escape as photons with V=c into the environment. Bosons are photons in scales < S9.
In S1-S7, due to the large gravitational distortion, the matrix has a
connection of forces that also act on the octahedra and tetrahedron in the
surrounding area. The energy of the 4D oscillations (time vector) of the
octahedra is interpreted by the matrix theory as
W bosons. It is the
normally "empty" octahedra that now become particles.
Gluons are bosons that
appear in interactions on scales <S1, i.e. S^-1; S^-3; S^-9. Of course,
these interactions are outside of naturally stable scales and are a result
of CERN research. There, research was confronted with the 4 parities of
oscillation in time and space, as described by the matrix theory. The result
was quantum chromodynamics, which mathematically represented the 3 colors of
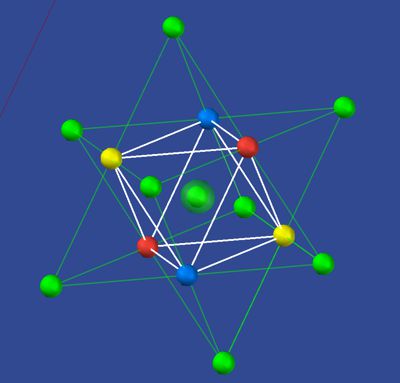
the octahedra described in the matrix in their 4 parities. The upper picture
shows the 3 colors red, blue, yellow with the disadvantage color green as
the total energy of the particle (here the octahedron).
 Hier
eine Darstellung aus "Quarks - Philoclopedia"
Hier
eine Darstellung aus "Quarks - Philoclopedia"
Quantum chromodynamics also shows the relationships between the 3 colors or parities of the 4D oscillation. Here as ++; +-; -+; and the resulting moment - - (as white in the center of the image). This representation arose from a series of experiments at CERN and the interpretation of particles and their properties.
The matrix theory knows no particles, only fields with coordinated oscillations, whose effects are seen as parities and not as static properties of particles in (empty) space. A parity always includes the opposite side of the oscillation, whereby the secret of antimatter is automatically solved.
In order to understand the role of the "empty" octahedrons in S1 / S3 as binding fields, 2 field associations are shown in the image below.
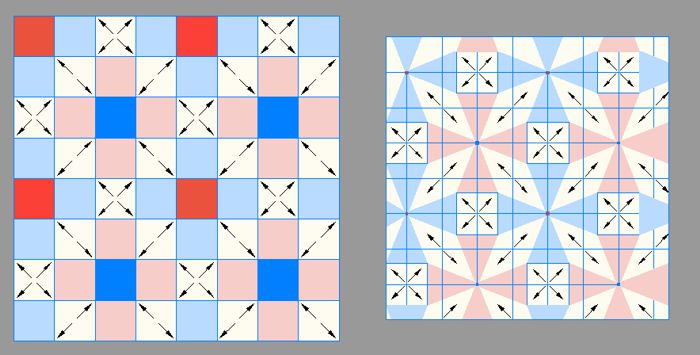
Left the Euclidean space of zero density is shown in symbolic form. The red fields (protons) form an association with the blue fields (antineutrons), which is kept at discrete distances and bonds with the contrary secondary fields. In the mixed fields, here white, the matrix is balanced in +/- and thus flattened, which means here attraction. It shows the phase (parity of oscillation in S1) where the proton has the so-called charge (SM) (+) and the neutron in the anti-neutron phase has the charge (-). The squares symbolize the octahedron of a layer. The arrows show the binding direction. The cross direction symbolizes the Z direction to the next layer. The overlaps form in S3. This compound, shown here only as an example, would show a state of matter that would be practically unbelievably hard and heavy. It could be black hole material, because singularity does not exist in physics, only in religion. Perhaps one day we will discover processes in the center of our galaxy that can be explained with this 5th aggregate state.
Right On the right we see the same image, but distorted relativistically. Protons and antineutrons are greatly reduced. The white fields show the binding effect. Note that the right image is smaller as a whole. This should be interpreted as a link to gravity.
The β-decay
A transformation of the β-decay with the field relations of the matrix is to be explained here. A view from the 4th dimension applies, where our 3D space becomes the surface in 4D space. It is assumed the vertical symbolizes the 4th dimension and the horizontal symbolizes 3D space. It is further assumed that the oscillations are seen as (+) only from the top view. A proton is an upward deflection here, it is the (+) parity of the proton for reference. As an oscillation, however, all representations can also be displayed horizontally mirrored.
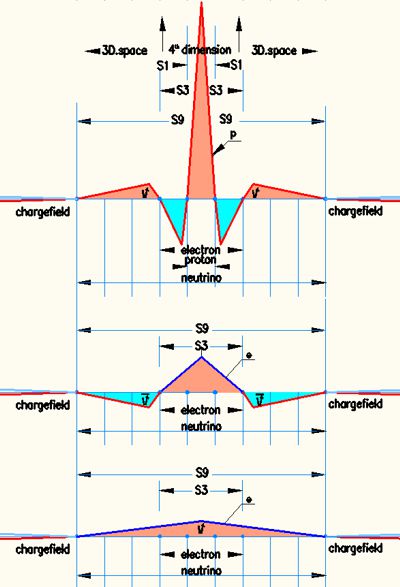
The picture on the right shows schematically the hierarchy of the elementary parts in the scale order of the matrix. To Oberst the proton as an impact from the 4th dimension S1 with the secondary fields S3, S9 and the beginning of the charge field of the electron binding. Red is (+) parity and blue is (-) parity.
In the middle, the free electron is shown in the same scheme. It is the impact from the 4th dimension in S3, the secondary field S9 and the beginning of the charge field of the electron bond.
The image below shows a weak impact from the 4th dimension in S5 and S7 as (+) and (-) in the same matrix scheme, with S9 only resonating and no longer receiving an impulse from 4D because the impact is too weak. The area S5-S9 therefore has no charge effect and is considered to be neutral as a whole. It does not cause a moment in the charge field S11 - S27. S5 - S9 is the scale of the neutrinos.
All fields shown consist of an impact of the 4th dimension as the primary field and the bound fields of the secondary fields in 3D space. They all therefore have V=<c.
This analysis of the matrix schemes revealed a most trivial flaw in the
physics of the Standard Model. In the understanding of physics in the 19th
century, particles were something solid and massive. Thus, in the course of
research, all of their observed behaviors were assigned to them as traits.
They were never space itself or its phenomena. The charge (+) was
arbitrarily assigned to the proton. After experiences in the electric and
magnetic fields, the properties (+) and (-) produced attraction. Since
protons and electrons attracted each other, the proton was seen as (+) and
the electron as (-). The matrix sees it differently. There are all repulsion
and attraction interactions of the fields surrounding the elementary
particle. The proton-electron interaction happens im S27 and forms there the
so called "electron
shells". The proton-electron interaction with the same center, a state of a neutron,
happens in the secondary field S3 and creates a very strong bond there,
which is probably only achieved in the formation of neutron stars due a
supernova explosion.
Since the secondary fields have an onion-shaped interplay of + and -, the
proton is the center of
- (+Proton+) -. The electron as counter-oscillation
would then have +
(Elektron +) +. In this way the electron would always
have the counter-oscillation to the proton in the interplay of the whole
space.
Here is a brief explanation of why it is easier to work with +/-.
The parities ++/+- are in + time and can be scientifically observed. The parities -+/- - are necessary for the oscillation of an entire cycle in 4D space, but we cannot prove them experimentally because they happen in - time. The reason for this is our cosmic situation, where we are in the timeline (start-finish) to the future. If we were to reverse the timeline, the world would be the same for us, we would consider ++/+- as antimatter and our universe would become smaller instead of expanding.
Here the Beta-decay:
Nuclear physics interpreted the process by β-radiation. It recognized
that with the energy of nuclear fission a proton can turn into a neutron.
Since this process changes the atomic number of the atom, a (β−) decay is
assumed at atomic number + 1 and a (β+) decay at atomic number -1.
(Physicists tend to complicate things). The (β−) decay then means that a
neutron becomes a proton (atomic number + 1) and with (β+) decay a proton
becomes a neutron (atomic number -1).
(β−) decay
n -> p + e- + ʋ- =
Neutron n=Neutron, e- = Elektron, ʋ- =Anti-Neutrino
(β+) decay p -> n + e+
+ ʋ+
= Proton e+ = anti-elektron (positron), ʋ+ =neutrino
This is where the space matrix shows its true face. The proton/electron interaction occurs in S3. There, however, the field is in (-) parity and the electron in (+) parity. Here only the parities apply, not the charge, which is actually only an idealized expression of a static description of particles, but is seen by the matrix theory as parities of oscillations.
The (β−) decay n -> p + e- + ʋ-
The proton (in the + field S1) receives an electron in its secondary
field (- field S3), an electron which is a + field in S3 at the same
frequency as S1. This neutralizes S3. The neutralized field S3 expands the
space there because of the neutralized energy (λ=h·c/E), which throws off
the secondary field S9 (-neutrino) belonging to the electron. It is ejected
by the high-energy interaction. The process in S3 will also have an effect
on primary fields S27, which would generate photons.
The (β+)
decay would
be done in the same sense with reversed parities.
In matrix field theory, only fields of the same scale interact. A proton therefore only interacts via secondary field S3 with the electron in S3. If the proton has parity (-) there, then an electron with parity (-) would be repelled. There would be no reason for such a bond. After all, a free neutron has a lifetime of ~15 min.
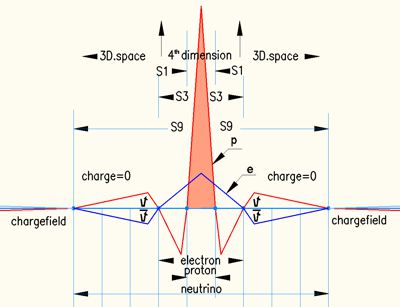
However, it is different if the assumptions of the images shown here apply. There "only" the S9 barrier would have to be overcome.
The formulas now look like this: Left image:
proton in S1+ ; S3- ; S9+
electron in S3+ ; S9-
neutrinos in S9 are only neutral space.
S3+-
becoms equalized
S9+- becoms equalized
What remains is a neutral
proton, now called a neutron.
Part 4 showed the application of matrix theory to nuclear physics. Further applications would lead to further research fields, which would go beyond the scope of this document.
What is approached?
The concept of a 4 dimensional space shows us a completely new type of field, which with its abstraction can be called a multiple field, a field of fields, which in turn consists of fields. This field explains the inner structure of the fermions. It shows the inner fields of the fermions, the primary field around the punctiform moment as an oscillation of the 4th dimension. This is followed by the primary field of the electron, the fields of the neutrinos, the charge fields or fields of electron orbitals, further fields of chemical reactions and all tensions of the electromagnetic space. The multiple fields show a concept that recognizes even the smallest particle as a field and extends this principle to gravitation. A principle that could unite all theories of physics. The basis of this explanation is the matrix as the geometry of a 4-dimensional space structure and the quantized vibrations of all existing things, which only become recognizable on a larger scale as analogous and static manifestations of our known world

Christmas 2016 I started to describe my idea of a space matrix as a web page "The field space". In 2017 and 2018, the ideas in my head and in my 3D CAD platform grew into a zoo of solutions that required a logical order. In July 2018 I started to document these ideas in a logical sequence with Word and picture. The individual topics produced themselves and amazed me with their surprising solutions. A new picture of physics grew, not conceived but seen.
Gunter Michaelis, Griesbach, März.2022
The vibration of the world-medium
The geometry of the medium space
The universe
Friedmann-space and the space-matrix
The space-time continuum
The space- and time-illusion
Particle in the matrix structure
The Electron
