the MATRIX of charged fields around atomic core
A determination of privileged locations of electrons, geometrically and without probability
 the
Neon-Atom
the
Neon-Atom
Abstract:
The paper describes the elementary charge as a geometric concept based on matrix theory. There are no shells, electron orbits or orbitals. It is based on the generally rigid but flexible scaled structure of the space matrix, the medium of which basically does not allow any movement. Instead, the concept of propagation is applied. As Bohr noted, it appears that a particle moving from A to B does not use the space in between.
Paradigms:
space
Matrix theory sees space as polydimensional. Whereby 3 dimensions is seen as the traditional space and the 4th dimension as time. But time is a human concept and does not apply to the subatomic scale. There time is seen as a geometric wavelength, the tensor value of an oscillation with a vector to the 4th dimension. This is the only way to explain the phenomenon of standing waves, which here is considered to be the physical existence of subatomic particles. This scale of space oscillates with parities of spatial density, which (under the influence of the Lorentz factor) generates a frequency of its ʎ values or wavelength in 3D and 4D space (3 and 4-dimensional space).
Oscillation
Matrix space is based on the idea that all space parts and cells are oscillations. Space it self is Oszillation. Its components like protons, electrons, neutrinos, bosons and photons are therefore oscillations by V=c (lighhtspeed). Since the very small ʎ-values (wavelengths) result in very high frequencies, this oscillation cannot be detected on our scale. Since these subatomic particles have significant relative differences in their ʎ values, the parities of oscillation appear as intrinsic properties (charge, chirality, helicity) of the oscillating fields, here seen as solid particles.
Charge
The arbitrary notion of charge is explained in matrix theory as the result (parity) of internal oscillation; A difference in the parity value (charge) arises from the fact that a proton is created at the same time fraction as an electron. Under the condition that only fields of the same size will interact, the field of proton only has the size of electron when its parity has changed. If the proton is on (+), then its secondary field is on (-) and interacts with the same (+) field of the electron. Since the oscillations are based in space itself, an electron always and everywhere has the contraverse value of a proton. Since frequency of the oscillation is higher than its detectability, in practical experiments we see here the charge as an intrinsic value of particles (not seeing an oscillation) and call it charge.
Picture 2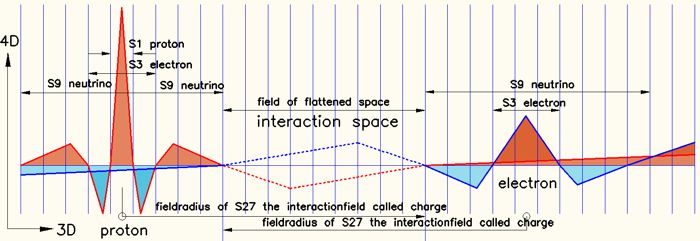
The concept of attraction or repulsion is explained in terms of the different spatial densities of two areas, which, by balancing (or flattening) the space, produces this phenomenon
the Geometry of space-Matrix
 Picture
3
Picture
3
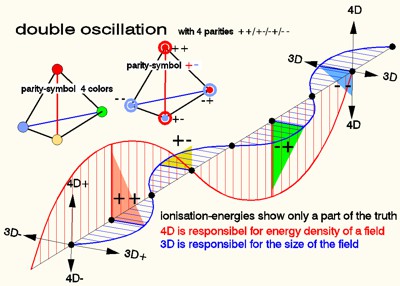
the oscillation to the 4th spatial dimension (4D oscillation) creates a punctiform primary field in 3D space, which is connected to the secondary fields through their oscillation. This creates a field with V<c, also known as a standing wave or as a soliton, which consists of 2 oscillations; one with vektor (tensor) in 4D and one in 3D. Both oscillations are one-dimensional string values. The 3D oscillation is a string with the freedom of 3 coordinates while the 4D oscillation is limited to only one coordinate. This is actually considered a good proof of the cosmic concept of a V=c expanding 4-dimensional universe as described by Marco Pereira, MSc in Physics, PhD in Physical-Chemistry in his HU theory. In a logical sequence, these 4 parities of the double oscillation form the tetrahedron space, which in my theory is explained as the geometry of the matrix the Geometry of the Matrix as the basic element of space.
Attraction und compelling in field space
The 4 dimensions of space allow a (non-visible) bending of coordinates in 3D space, which is mathematically verifiable as the Lorentz factor. Significance of this bending, however, can only be seen at a cosmic or subatomic scale. While at the cosmic scale it is recognized as gravity, at the subatomic scale it is the general attraction of all particles. Since the bending of space can be very strong there, it interacts with the entropy (general density) of space, causing the +/- interaction (cancellation) to reduce density (stress) and inflate space; Interaction
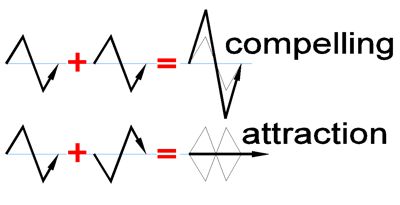 Picture 4
Picture 4
The picture systematically shows the compressed and the flattened
space as the cause of repulsion and attraction. Entropy causes motion toward
flattened space. Culminated warping causes repulsion.
All forces of
attraction and repulsion can be interpreted as a rebalancing of space
density. In matrix theory there is no arbitrary assignment of properties
such as charge or gravity without a geometric explanation of balance.
Fieldsizes
All field sizes have discrete quantized values.
Those in 3D space obey
the law λ=h·c/E
and that of 4D space λC = h/(c·m) ( λC=Compton
wavelength)
E=energy, h=Planck auxiliary*) variable, m=mass and c=speed
of light.
If the 4D impact for the proton in matrix space is set to size
1, the electron has geometric reference size 1/3, the neutrino 1/9, and the
subsequent field of electron interaction (called the charge field or atomic
shell) has size 1/27 However, since the curvature of space is a significant
quantity on these scales, the distances are strongly distorted according to
their energy (rest mass). The Compton wavelength shows the true proportions.
λC = h/(c·m), where m=mass.
Electron : λC,e = 2.426 × 10^-12 m E=0.511 MeV
Proton
: λC,p = 1.321 × 10^-15 m E=938.3 MeV
Neutron : λC,n = 1.319 × 10^-15 m E=939.6 MeV
German="hilfs"-Variable, thats why Planck called it h
In general, the geometry of the matrix, which is only a benchmark, applies
here. Due to the influence of the electrical effect (λ=hc/E), the distances
as λ (rod lengths) of the Matrix hold a certain amount of energy. If its
energy difference is more than one quantum, these collapse into a smaller
scale such as S4 to S3 etc. But usually the field sizes also have a certain
meaning such as: neutrino as S5 or neutrino as S7 or neutrino S9 for
octahedron. Nuclear physics shows us neutrino S5 and S7 as + and - valence
fields together. S9 no longer has a mass. However, the neutrino needs the
whole area S5 – S9 in the resonance metric of Matrix. This explains the
neutrality of neutrinos with speed V=c of photons.
The Lorentz factor has a
different influence to the rod length (λ), when mass or potential energy
(eV) is involved. The benchmark value of the Matrix e.g. between electron
and neutrino (S3 / S9) is 1/3. The value of the rest masses or potential
energies is e=511 eV / n=0.8 eV = ~639 larger. The difference between the
benchmark and the energy value = 639/3=213. The application of the Lorentz
value reduction should show a curve with a steep of 1/213 on the diagram. By
this shortening of 1/213=0.0047, the neutrino rod length would fit into the
secondary field of the electron, as required in the benchmark Matrix. The
whole scene must be imagined as if the potential E values (mass) are the
steepness of mountains when everything is seen from satellite.
Interaction of charge fields
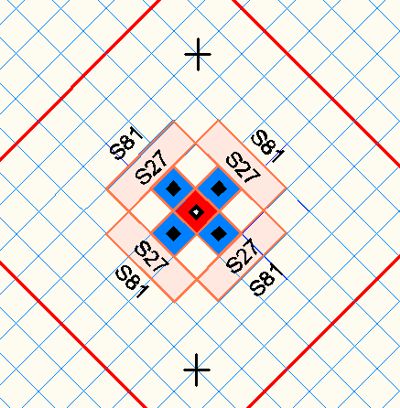 Picture 5.1
Picture 5.1
With the geometric structuring of space (Matrix) in tetrahedrons, it is divided at equal intervals (bar lengths). Different scales are generated at different forces. These are explained in detail in my page Matrix: Matrix: Fields of Electric Charge
The pix shoes a proton S9 parafield, a field with a proton in it and surounded by S9 fields with electron in it. The overlapping are mainly happend in S27 sized fields. Here it is Chromium (A.Nr.6).
Here is an important difference between Matrix theory and accepted physics. The charge fields as secondary (or para) fields of electrons do not rap arround the charge field of a proton, i.e. do not have the atomic core as their center as the orbits of the Standard Modell have, but they bind at the field S9 (in the field-overlap S27) of the proton. As a result, the inner fields of electrons remain outside the effect of the inner proton fields, where they otherwise would form neutrons instead photons, what is the ionisation energy. This case (neutron star) occurs only under highest gravitational influence where high energy walls (Pauli´s exclusion) collapse as a barrier. The idea of ORBITALs wouldn´t fit in the picture. E.g. in orbital S1 an electron had to share a too close place to a proton.
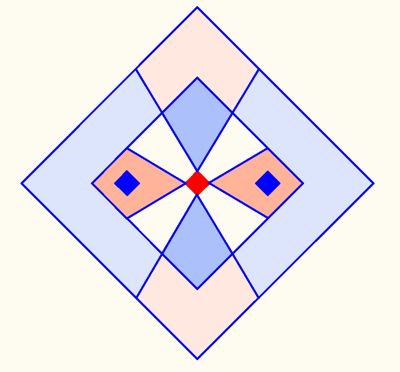 Picture 5.2
Picture 5.2
Within the range S27 and S81, the matrix distances are theoretically not curved and flat. Since the curvature forces of space (due to its high density) are considerable at the subatomic level, the matrix-directed distances are strongly deformed. The geometry of the matrix is only a gauge geometry there. From S27 onwards, however, spatial deformations due to gravity are hardly recognizable. However, the matrix as a scale shows the relationships of the privileged places for electrons, which interact with their own field S27 with that of the proton S27 and partially cancel each other out. During the interaction, the binding energies (ionization energies) are added or subtracted and thus their field sizes change (λ=h﮲c/E). They become severly deformed by electromagnetic forces. This process is very complex and makes explainations by ionization energies only in special cases possible.
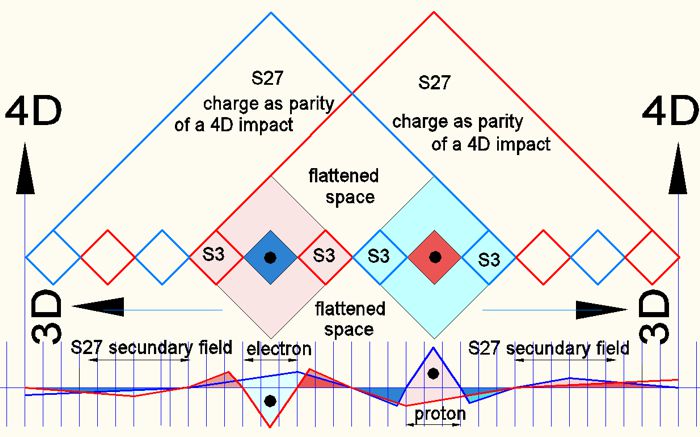 Bild 5.3
Bild 5.3
The image shows the interaction when the field areas S27 overlap in the secondary field S81. The upper part of the image shows the overlap in the 3D plan. The lower part shows the field overlap with the 4D coordinate (energy density). In the upper part (middle) the change of parities in the matrix of the medium is demonstrated. It must always be remembered that the fields are in the parity rhythm of the matrix (either in (++)/(- -) or in (+-)/(-+). The first sign (++) is the 4D parity, the second sign (++) is the 3D parity. What is referred to as the physical part of our 3D world. All fields there arise through 4D influence in the 3D boundaries of the matrix.
The binding energy
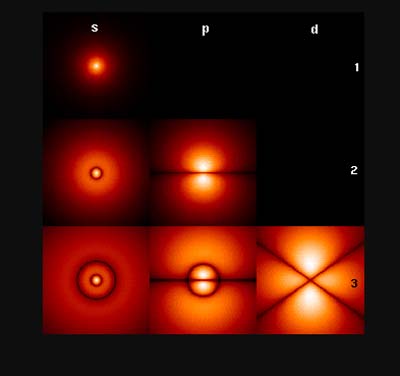 Picture
6 shows calculated ranges of probability according to Schrödinger, called
orbitals.
Picture
6 shows calculated ranges of probability according to Schrödinger, called
orbitals.
Also known as ionization energy. This energy applied to the periodic table and clearly shows the relationships of the groups of 2 and 8 of the electrons on the shells around the nucleus. These relationships cannot really be explained by circles on a 2D plane. There the valence electrons have a weak binding energy (p﮲λ), the values of which depend on the one hand on their relationship to the group of 8 and on the other hand on their distance to the nucleus. It is often argued that the electrons in the inner “shells” are in the way, making the ionization energy weaker. However, the opposite is the case, as the measured values in the list down below will show. Also the use of orbitals, the assignment of 4 quantum numbers, the calculation of the areas with 90% probability by the Schrödinger equation says nothing about mutations of energy of the binding energies.
Picture 7
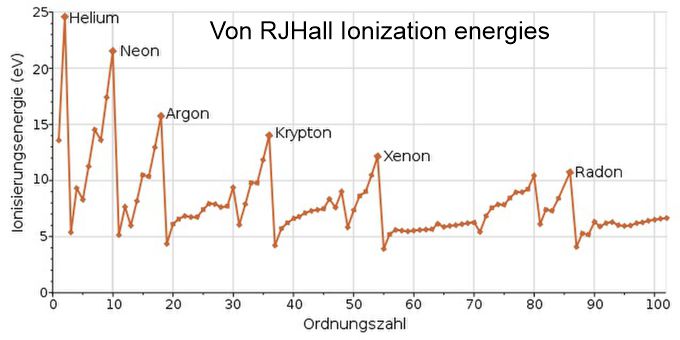
A prima vista we see the periodically appearing of peak values, which
point to the atomic number of the noble gases in the table. Here 2; 8; 18;
36; 54. After Xenon (54) it becomes unclear. The opinion of mainstream physics,
that ionization energy depends on the distance to the atomic nucleus, is
obviously only part of the truth, which is why no corresponding 3D model for
it has been found so far. The formula of distribution as numbers of
electrons = 2 x shell^2 does not seem to be experimentally supported.
It
should be pointed out here briefly to the latest state of physics.
An electron is
said to have 4 quantum numbers (Qn):
Qn 1=n=the horizontal row 1-7 of the
periodic table
Qn 2=l=secondary quantum number, the shapes of orbitals;
l0=s=circle; l1=p=Handel; l2=d=crossed handles.
Qn 3=magnetic quantum
number (+) or (–) in all 3 directions of 3D space x;y;z
Qn 4 spin
quantum number +1/2 or -1/2.
The spin quantum number makes the biggest
difference to the explanation by matrix theory. Mainstream physics actually
uses the spook of a double occupation of a point in space in the sense that
an electron can share the same point in space with another electron.
Normally, spin should mean a twist or rotation. Here, however, it is assumed
that an electron of its full rotation time 1 only exists one ½ rotation and
can share time/space of the other ½ rotation with the existence of another
electron. This is illogical since a rotation has an axis that can have
almost infinitely many 3D angles and thus 2 rotations never cancel each
other out. The quantum number
Qn4 was obviously invented to make the
Schrödinger formula work. All of these quantum numbers therefore arose from
the analysis of the atomic shell structure and correspond only
approximately to experimental research. In order to completely replace the
idea of quantum numbers, the 4 field moments (parities of a cycle of 720°)
in the matrix
theory are used here. Instead of quantum numbers, we use
(++) (+-) (-+) (-
-), the 4 colors of the matrix.
The geometry of the space/time matrix offers a different solution here,
which corresponds to the ionization energies of electron shells. The
starting point is the noble gases, which seem to be the most stable
combinations. The geometry of matrix shows a solution where the privileged
space points of the atomic shells consist in groups of 2; 8; 18. These arise
from the shape of octahedrons, which form the weakest link of the spatial
structure in the matrix. This emerges from the matrix theory, which assumes
an impact with a 4D tensor for particles, which then has a 3D effect in the
weakest point of the spatial structure for simple static reasons. The
geometry of octameters explains the group formation of the electron sites.
Here is the exact listing:
Atom number 2 = 2
Atomic number 10 = 2+8
Atomic number 18 = 2+8+8
Atomic number 36 = 2+16 2+16
Atomic number 54 = 2+16 2+16 2+16
Current
physics assumes that the orbitals s, p, d, etc. are filled. However, with
its variety of orbitals, this creates a lot noble gas configurations, which
does not correspond to the table of ionization energies. There, the electron
numbers are energetically very close to one another, but have an abrupt jump
(drop from high to low values) in there binding energy, when the number
changes to the one of noble gas. These drops in binding energy (atomic
number 2-3 or 8-9 etc.) can only be explained by a dynamic component (here
the loss of symmetry) of binding energy. Physics describes it as a magnetic
quantum number. It is a value as a place-filler for the complete description
of the electron, i.e. here a property. In matrix theory explanation it would
be a parity of an oscillation. It's the old story: SPIN or parity. The
matrix space does not allow rotation within itself on a quantum scale, since
every movement is interpreted as propagation and quantized space. The
infinitely small steps of a movement would produce infinitely high energies
with E=hc/λ and thus a paradox. The Matrix strictly insists on a consistent
geometric explanation. The oscillation of the electron with all its
secondary fields creates charge moments that cancel out with the central
nucleus. As long as the number of electrons has not reached that of the next
higher noble gas (2; 10; 18; etc.), the moment of charge oscillation acts as
an instability. When a new electron is added, not only the position of the
best symmetry is chosen, but also the position of the strongest interaction
(normally in S1 to S9 as gravity). The noble gas configuration has then
achieved full symmetry.
The Beta+ decay (ß+)
In the case of beta+ decay, a phenomenon that occurs when a white dwarf collapses, the process can be described as follows: It is assumed that the pressure inside a white dwarf becomes so great that the Pauli barrier of S3 (the region around the proton with the energy of an electron) collapses and the electron occupies the parafield S3 around the proton. The result: In the S3 region and S9 around the proton, the parities are neutralized and a neutron is created, a proton without its parafields (of charge, spirality, etc.).
The standard model: ß+ = p(+) + e(-) = N(o) + e(+) + ν(antineutrino)
this means: 1 proton + electron becomes a neutron + positron + antineutrino
and described by the matrix or the parities of the double oscillation
this means: ß+ = p(++) + e´(+-) + ν´(+-) =
N(++) + e(-+) + ν(-+)
Here the parafields count from the beginning. e´(+-) + ν´(+-) are parafields of the proton. With this notation, no new particles are created, they are released into the environment as energy, as parity moments.
Due to the historical tradition of discoveries made at different times, the Standard Model has a number of criteria that are difficult to correlate. These are listed here:
Spin --------------------------------- twist of 720°, reduced to 360°,
that´s why 1/2 Spin
Chirality, Helicity-------------------turning left-right in 3D.space (handrule)
Antimatter --------------------------all quantum values (incl. time)
are reversed
Charge ------------------------------inner properties of
fermions
At least Dirac was able to derive his spinors from this misery. All
these values with naive names now had a mathematical context. The matrix
theory also derived the 4 moments in 4D space as signs of the spatial
density, (++) (+-) (-+) (- -) or as colors
(++) (+-)
(-+) (-
-)
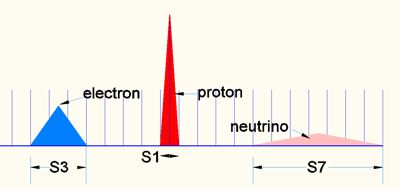 picture
8
picture
8
Here the 3 particles are derived from the SM (Standard Model). Vertically the 4D moment (E) and horizontally the relative field size. The values here are symbolic.
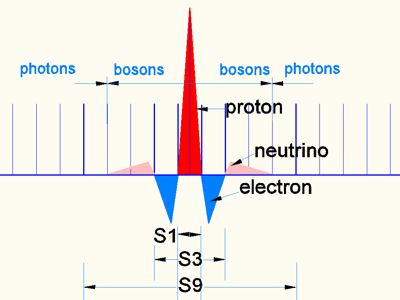 picture
9
picture
9
It shows the proton (red) with the electron para-field (blue) and the neutrino para-field (light red). Para-fields are the logical consequence of the matrix. Here they correspond to the formula λC = h / (c · m0) of the Compton wavelengths.
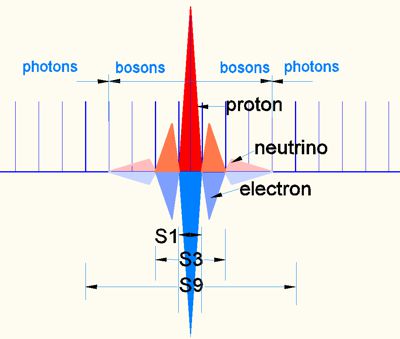 Bild
10
Bild
10
The para fields of the entire cycle of the double oscillation are shown here. All fields and para-fields cancel each other out energetically. This process continues in size until no more bosons are formed in S9 and EM oscillations of photons escape into the EM space. However, these oscillations are neutral and could be responsible for the very weak gravity there.
The privileged places in the Matrix
For the sake of clarity, the following images show the geometric connection between the privileged electron sites as overlapping 1/3 or 2/3 of S27 fields (picture 5.1).
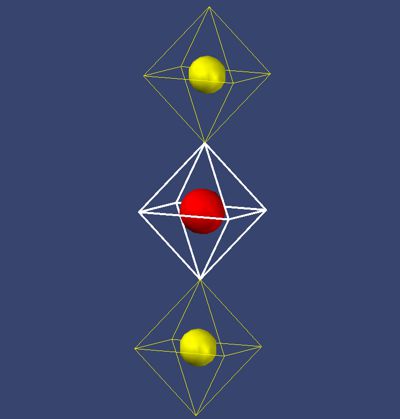 Picture
11, the helium atom
Picture
11, the helium atom
Here another phenomenon of electron binding should be
explained. The docking of electron field (S9) is only part of the picture.
As will certainly be noticed, according to the matrix theory, docking does
not yet produce any attraction (Fig. 2), only overlaping. Here the invisible
field S27 overlaps by 3/9 of its capacity. We have to consider the fact,
that the electrons here (yellow) have the same parity. That means, charge is
not the only cause of attraction. There are 2 forces who cause attraction:
1. gravity 2. parity or in physics called charge. Gravity comes from the
4D-impact and is in these scales much stronger then 3D oscillation of
density of these fields. In far distance an electron is much more attracted
by the force 1 then by force 2. That is the reason, that the first 2
privileged places don´t apply the charge rule (+/-).
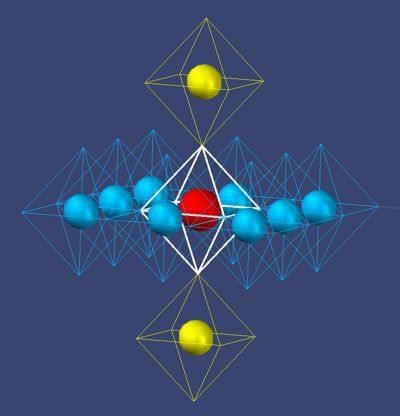 Picture
12 neon
Picture
12 neon
The picture shows the neon atom with 10 electrons (2 + 8). Another
aspect of the behavior of electrons in the atomic shell is to be described
here. Despite the general attraction of the atomic nucleus in the center,
electrons are very hesitant in choosing their place. This is because
electrons have to make their way through the secondary fields outside of the
shell, which are not shown here. The whole dynamic is based on balance. An
electron is thus attracted from a great distance in waves, i.e. it passes
through (weak) zones of repulsion and attraction until the valleys and
mountains near the nucleus become so steep that the electron levels off in
S27 of the nucleus and stays there.
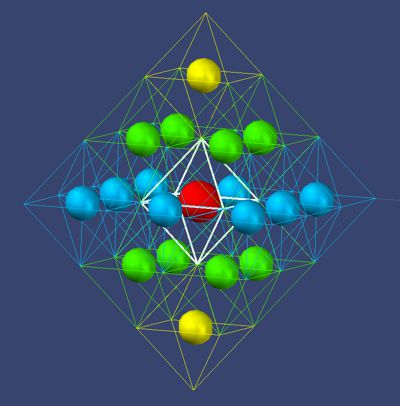 Picture
13 argon
Picture
13 argon
Its composition here is 2+8+8 = 18. This again achieves the overall shape as
an octahedron. As a general finding, the choice of place of the electrons
can be seen as follows: an electron always first tries to find a place in
the middle-field with 8 places, that is as far as possible from occupied places, but on the other hand
forms the best possible symmetry. The best symmetry results in noble gas
configurations. The electron that comes after it therefore only gets a very
asymmetrical place, which is unstable and has only an extremely small
ionization value The best symmetry results in noble gas configurations. In
addition, another variable of attraction is the bond combination. Here are
the combinations of the 4 parities as moments from 4 spatial dimensions:
(++/+-) (+-/++) (-+/++) (- -/++)
(++/-+) (+-/-+) (-+/+-) (- -/+-)
(++/- -) (+-/-
-) (-+/- -) (- -/-+)
The parity force in combination with gravity results
in the ionization energy in addition to the geometric configuration. The
noble gas configuration is the combination where all three forces have their
maximum, whereby an octahedral shape is aimed for.
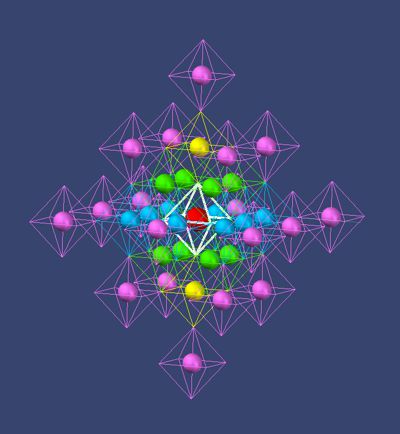 Picture
14 krypton
Picture
14 krypton
Its electron count is 36 and should have the following geometric sequence: 2; 8th; 8th; 18. The electrons shown are blue, green, yellow for argon and violet for krypton. As can be read in the ionization table, 2 places Top and Down were booked first. Then the 8 places at the equator (very closely spaced ionization energies) and finally the filling of the north and south areas (always in diagonal occupation according to the table). It must be pointed out the complexity of the charge field, which changes as a whole with each further occupation.
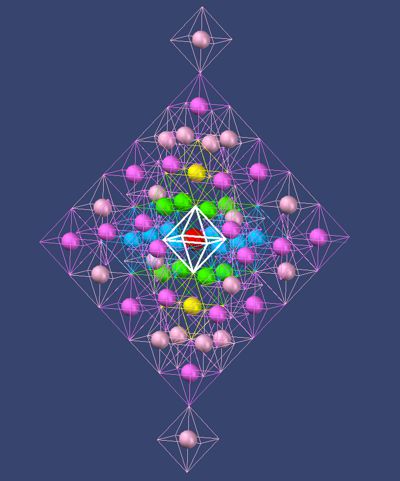 Picture
15 xenon
Picture
15 xenon
Its electron count is 54 and should have the following geometric sequence: 2; 8th; 8th; 18; 18. The last groups consist of 2 + 8 + 8 = argon + 2 + 8 + 8 = xenon, which can be read in detail from the ionization table (with some practice). Up to xenon, the noble gas formations correspond to the rows of the periodic table. Radon is disturbed by the series of lanthanides in its geometry of the octahedron and then the atomic number of the natural elements ends prematurely. It is assumed here that another layer around the octahedron of xenon holds potential places. In the theory of the geometry of the octahedron, the next layer after xenon has 146 places, with 2 places already occupied by xenon. However, the atomic numbers of the natural elements do not go that far. A stable longevity cannot be expected here.
Field overlap 1/9 of the S27 fields according to Figure 5.2
Theoretically, field overlaps in S9; S27; S81 or higher happened. The choice of the above images is based on Figure 5.1, where field size S9 only touches, but S27 overlaps 4/9. However, this condition is only to be expected in a star like the Sun. Even denser field overlaps (1/9 with S9) are probably expected there, since neutrinos (field size 8) are produced in the sun. The normal field overlap in normal conditions like those on Earth have the field overlap analogous to figure 5.2. However, this is geometrically very complex and was not used in our examples. The type of overlap has no influence on the result, a clear geometry of octahedra.
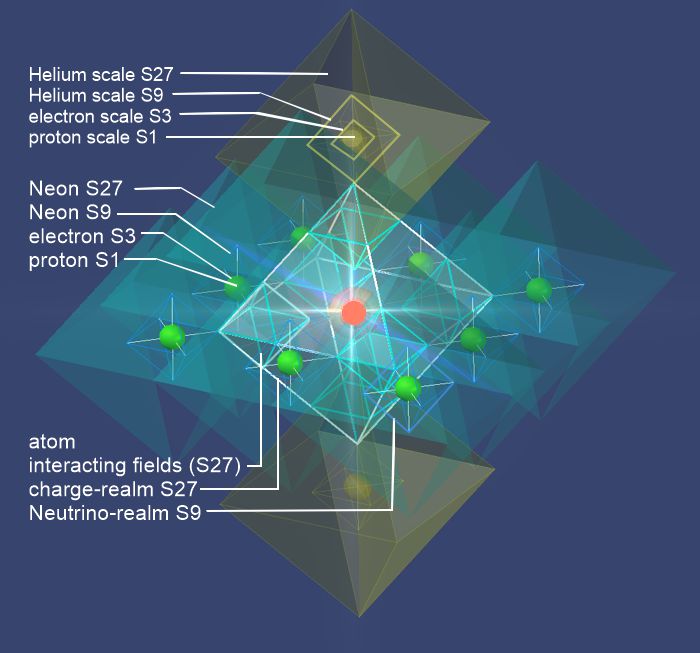
Here the fields S27 of the electrons are shown. The S9 fields around the electrons are also very weak. The central octahedron in white is S27 of the atomic core. in this S27 the overlaps (small white octahedra in size S9) can be seen. The picture shows the neon here.
Which elements of school physics can be taken over, which will be replaced?
The 4 quantum numbers can be partially adopted or replaced.
Value
Qn1 - Qn7 corresponds to the groups of occupation or here shown as
colors (5 colors for xenon) and also levels of the periodic table. But
shells can't be used.
The value Qn2=l cannot be accepted
since it corresponds to the idea of a dynamically moving system. The
question arises whether Q2=l is necessary, a simple look at the periodic
table tells us all.
Value Qn3=magnet-quant will be
replaced by the torque caused by its momentum of the whole system. Only
asymmetrical places cause a moment, which change the center of mass compared
to the geometric center of mass by a dynamicly filling. A new torque then
will be created.
Value Qn4=spin. This value is omitted
because the formula Qn1 x (Qn2)^2 has been proven to be wrong. Since the
spin creates an axis and this axis would have to adapt with each new
electron, the matter becomes paradoxical. The parity explained above is
simpler and would also produce the same result in the Stern Gerlach
experiment. However, the parity of an oscillation of electrons would be here
a function of space itself. The difficult idea of axes in the quantum salad
would not be necessary.
It should be remembered here that in space matrix all octahedra are only
"empty" spaces in the tetra structure of space and, as the weakest link in
the medium "space", absorb the impulses from the 4th space dimension. That's
why fermions (here the electrons) are the center of octahedra. The
octahedron itself is the first field. Further fields up to the fields of the
"charge" are again octahedra, which lie symmetrically around the original
field. It all oscillates fully in harmony.
The oscillation of the
electrons in the matrix always and everywhere in the space matrix have
opposite parity to protons. All "empty" surrounding space cells oscillate
everywhere as tetrahedra in 4 parities=>
(++) (+-) (-+) (- -)
For a deeper understanding of matrix theory, I recommend my other papers of MATRIX theory.
The MATRIX of all what is
The vibration of the world-medium
The geometry of the medium space
The universe
Friedmann-space and the space-matrix
The space-time continuum
The space- and time-illusion
Particle in the matrix structure
The Electron
Gunter Michaelis, Griesbach den 27.2.2023, rev. 02.01.25
