Wie entstand das Medium der Matrix
Hier werden Begriffe verwendet, die in Oszillation erklärt werden.
Willkürlich wird angenommen, dass wir existieren und das Universum einen
Anfang hat. Dieser ist sehr wahrscheinlich nicht absolut. Er ist wie der Anfang
eines Tages, der auf den vergangenen Tag beruht. Nach der Geburt des Universums
ist alles andere nicht mehr willkürlich sondern deterministisch. Am Anfang wird
ein Szenarium wie der Big Bang der (immer weniger) anerkannten Theorie sein. Die
unvorstellbaren Kräfte, die extreme Kompression des Raumes, unermessliche
Temperaturen und eine Zeit-Dilation ins unendliche lassen erwarten, dass nur
Konfigurationen von Zuständen höchster Harmonie überlebten. Im Prinzip fand der
Raum selber seine idealste Konfiguration wie:
1. Dichteste Packweise des
Raumes (Matrix-Struktur)
2. Ein Zyklus kaskaden-mäßig geordneter Mini-Zyklen
der Zeit in (+) und (-)
3. Die perfekte Balance der Momente
Kompression/Dekompression
So konnte sich das Universum dem Physiker als
leeren Raum präsentieren. Keine Asymmetrie der Kräfte, sogar Licht war in die
vollkommene und perfekte Harmonie der Konfiguration eingefroren. Nachdem das
Universum expandierte, blieb die ursprüngliche Konfiguration in den kleinsten
Bereichen, die Lücken die die Expansion schuf, wurden mit neuen Freiheiten (nach
Feynman) aufgefüllt. Explosionsartig füllten sich diese Lücken mit Hitze,
Licht und Bewegung. Der übrige Verlauf ist uns ja bekannt. Ein Geschehnis wurde
jedoch noch nicht erwähnt: Der Kollaps der Stabwiderstände (der Farbabstände) in
der Größenordnung M1; M2; M3 (Metrik der Maßstäbe), der die Fermions als
Oszillation mir Vektor zur 4. Raumdimension erschuf.
Mehr Information in Metrik und Maßstab
Die Dynamik der Matrix
Der Begriff MATRIX ist eine räumliches Netzwerk, das aus Tetraedern mit
inneren Abständen in der Form von Oktaedern besteht, skalierbar ist, die
Zeit in 2 Richtungen einwirken lässt und eine Elastizität besitzt. Da
angenommen wird, dass auch Physiker mit lesen, sei bemerkt, dass
grundsätzlich der
 Euklidische Raum benutzt wird. Dieser jedoch ist nicht
isotrop und wird in dem Sinne angewandt, dass im Maßstab der Partikel mit
Einheiten der Stablängen des Protons (im Bereiches ihres Kollapses), im
Bereich der Felder mit den Einheiten der Metrik (des jeweiligen Maßstabes)
und erst im Bereich des EM-Raumes mit Quanten im Euklidischen Raum gerechnet
wird. Das räumliche Netzwerk der Matrix ist in allen Bereichen die
Grundstruktur, wird jedoch in seiner Auswirkung bei größeren Maßstäben immer
unwichtiger, seine Anwendung endet bei den bekannten analogen Größen, bei
denen je Bedarf der relativistische Raum angewandt werden kann.
Euklidische Raum benutzt wird. Dieser jedoch ist nicht
isotrop und wird in dem Sinne angewandt, dass im Maßstab der Partikel mit
Einheiten der Stablängen des Protons (im Bereiches ihres Kollapses), im
Bereich der Felder mit den Einheiten der Metrik (des jeweiligen Maßstabes)
und erst im Bereich des EM-Raumes mit Quanten im Euklidischen Raum gerechnet
wird. Das räumliche Netzwerk der Matrix ist in allen Bereichen die
Grundstruktur, wird jedoch in seiner Auswirkung bei größeren Maßstäben immer
unwichtiger, seine Anwendung endet bei den bekannten analogen Größen, bei
denen je Bedarf der relativistische Raum angewandt werden kann.
Nun sind hier schon einige Begriffe benutzt worden, die in der Page
MATRIX näher erklärt und hier nur kurz nochmal begründet werden.
Die Tetraeder-Struktur wird im MATRIX Teil 1 erklärt. Im Sinne eines Equilibriums werden nur die Tetraeder angeschaut. Die Oktaeder sind nur Zwischenräume. Im Sinne des Kollapses der Stablängen jedoch werden nur die Oktaeder betrachtet, da es ihre Diagonalen sind, die kollabieren. In der Physik werden sie Quarks genannt.
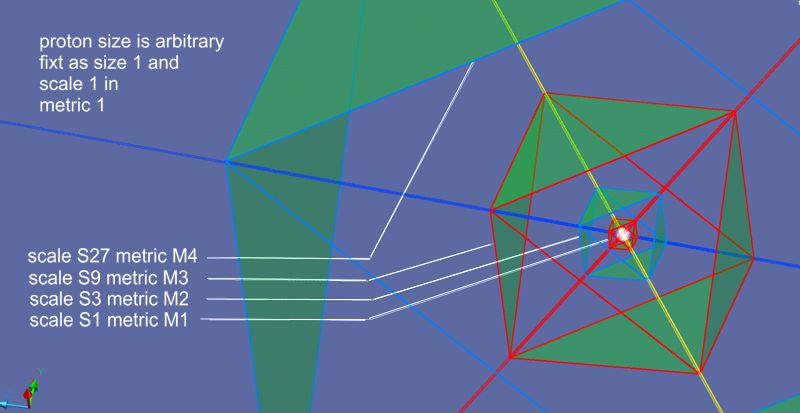
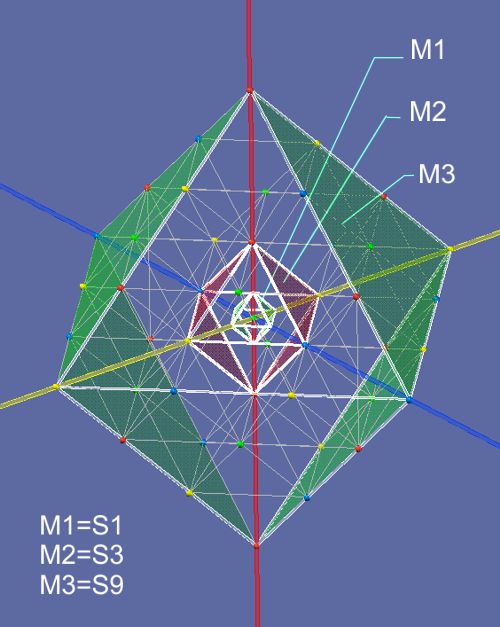
Das obere Bild zeigt die verschiedenen Einheiten der verschiedenen Maßstäbe. Der Impulse, der von der Oszillation eines Protons in den 3D-Raum emittiert wird, wird hier in der Größe S1 zum Quant. S1 ist daher h/pulse. Puls ist hier nicht mc^2 und nicht zu verwechseln mit den Energien dieser Oszillation mit Vektor in die 4. Raum-Dimension. Er ist nur die Nebenwirkung dieser Oszillation und nur im 3D-Raum der Größe M1. Da dieser grundsätzlich experimentell erreichbar ist, sollte ein Wert hier gefunden werden. Dies ist eine Aufforderung an die Physiker. Da S1=M1 ist und das Ladungsfeld der S-Schale M6=S243 ist, könnte ja hier ein Quant analysiert und auf das Quant S1 angewendet werden. Im Moment kann nur mit Relativ-Werten gedacht werden. Die Frage bleibt offen, ob nicht mit der hohen Frequenz dieser Oszillation die Quanten im 3D-Raum sich stapeln, da ihre jeweilige Länge abhängig von ihrer Metrik und der Energiegröße eine kleinere Frequenz fordern als die der Oszillation des Protons.
Hier ein Beispiel: Gegeben wäre die Frequenz 10^10 für die Oszillation des Protons, diese erzeugt eine Beugung im 3D-Raum, was ein Quant mit einer zugehörigen Frequenz (S1=c/F) F=10^8 erzeugt. Es bildet sich ein Stapel von 10^10-10^8=10^2 Quants. Hier wird angenommen, dass sich dieser an der Peripherie von S1=M1=Sphäre = πd^2 = 3 entleert. Von dort wird sich der Stapel (100-3=97) in M2=S3 entleeren, wo sich wieder an der Peripherie = Sphäre = d^2π = 27 die Quanten entleert hätten, wenn die Quantenlänge gleich (S1) wäre. Da in M2=S3 die Länge des Quants 3 mal so groß wie Quant M1 ist, entleert sich hier der Stapel nur um 27/3=9 Quants. Die Zeit jedoch für die Entleerung ist nun ebenfalls 3-mal größer, was eine Kompensation der Entleerung in M1 um 3*100=+300 Quants den Stapel wieder vergrößert. Bei M3=S9 ist die Entleerung π9^2=254, die Zeit 9-mal länger mit einer Kompensation in M1 von +900 Quants. Bei M4=S27 ist die Entleerung π27^2=2289, die Kompensation in M1 jedoch 27*100=2700. Es ist abzusehen, dass von M5 an die Entleerung grösser wird als die Kompensation in M1.
Das Beispiel zeigt einen großen Denkfehler, der gleichzeitig sich auf eines der tiefsten Geheimnisse der QM begründet. Aus der Oszillation des Protons fließt keine Energie. Die Interaktion des Protons als Oszillation zum 4D-Raum mit den Energien des 3D-Raumes geschah prinzipiell viel früher, theoretisch sogar bei der Geburt des Universums. Sie bildet ein fixes QM-System, wo die Pulsgrößen entsprechend der Metrik, in der sie sind, ein fixiertes Verhältnis ergeben, dass keine Energie verliert. Es kann sich ein idealisierendes Bild aus „stehenden“ Wellen vorgestellt werden.
Die Hierarchie der Felder
Man kann auch von der Hierarchie stehender Wellen sprechen. Zuerst der
Begriff Matrix im Zusammenhang mit Feld und Welle.
Der Begriff Matrix
besteht aus Raum-Zeit und Puls, wobei Puls in zusammengesetzter Form auch
Energie bedeutet. In der QT (Quantentheorie) werden die Größen bzw.
Portionen Raum, Zeit, Puls in definierten Beziehung gestellt. Jeder Raum
besteht nicht mehr aus x,y,z sondern aus der Einheit des Raumes, eine
Portion, die ebenfalls Raum ist und in bestimmten harmonischen Verhältnissen
zu den über- und untergeordneten Raumzellen steht. Diese Portion bekommt
hier ein Bezugswert zum Raum des kleinsten Feldes um das Proton. Z.B. das
Feld mit der Metrik M1 und der Größe des Maßstabes S1. Mit den definierten
Raumportionen werden entsprechend der QT auch Zeit und Pulse definiert.
→
Zeit t= r/c wobei c=Lichtgeschwindigkeit und r=Radius der Feldgröße ist.
→
Pulse=h/r h ist die Planck-Konstante, r=Radius der Feldgröße ist.
Jede
Raumgröße hat deshalb ihre eigene Metrik, eigene Zeit und eigenen Puls. Die
Hierarchie der Raumgrößen ergibt daher auch eine Hierarchie der Zeit- und
Puls-Größen z.B. S9 = M3 entspricht seiner Einheiten Zeit=T(M3) und
Puls(M3).
Die Matrix ist daher nicht nur eine Raumstruktur, sondern ein
harmonisches Zusammenspiel von Raum-, Zeit- und Pulse-Portionen in der
jeweiligen Metrik.
Die Darstellung der Metrik in der Matrix-Struktur
Es wird oft vergessen, dass die Matrix aus Tetraeder
besteht, die in ihrer Volumen-Füllung ein Muster von Abständen mit der Form
von Oktaeder ergeben. Dies ergibt ein Bild, das als eine nahtlose
Raumfüllung aus Oktaedern oder aus Tetraeder gesehen werden kann. Die
Einwirkung der 4. Raumdimension zwingt uns, die Tetraeder als Träger der Raumpunkte zu sehen, die im Equilibrium
Null als Summe ergeben. Damit werden die Oktaeder zu Löchern im Raum, die im
Kollaps der Struktur ein bestimmten Statuswert (++ +- -+ --) bekommen. Wenn
der 3D-Raum als 2D-Fläche gesehen wird, dann passiert dort die vom
Raum-Kollaps verursachte Aufbiegung in den 4D-Raum bzw. in die n-Koordinate
des 4D-Raumes (x:y:z:n). Bis dahin ist noch alles beschreibbar.
Nun
sollten die Kriterien Zeit und Puls bzw. das Moment h der Struktur
zugeordnet werden. Als erstes werden den Raum-Punkten die 4 Statuswerte (++
+- -+ --) als 4 Farben zugeordnet. Es entstehen die ersten Regeln:
• Im
Sinne eines Equilibriums darf keine Farbe gleich seiner Nachbar-Farben sein.
• Im Sine der Energie-Ausbreitung sollte jede Farbe gleich sein
Die
Geometrie der Matrix regelt die Sache so: Wird der Raum mit Tetraedern der
Seitenlänge 1 (willkürliche Annahme) gefüllt, dann ergibt diese Saitenlänge
bzw. Stablänge S1 ein vollkommenes Equilibrium. Wird in der gleichen
Struktur die Stablänge S2 angewendet, dann wird bei jedem Raumpunkt immer
der gleiche Raum-Status (Farbe) gefunden. Der Raum wird so leitfähig für
alle Störungen bzw. Energien. Dies zeigt uns, welche Wirkung die Stablänge
hat. Im Detail wird das im Teil 1 der
MFT Teil 1 behandelt.
Bei der Erklärung subatomarer Vorgänge muss nun auch der Moment
h als
eine universale Konstante in die Matrix-Struktur eingebracht werden. Die
Mitspieler bei dieser Lösung sind die harmonischen Beziehungen der einzelnen
Frequenzen. Der Begriff Frequenz wurde daher schon im vorgehenden
Artikel und im Link
Oszillation
erklärt.
Jeder Raumpunkt bzw. jede Farbe ist eine Oszillation, die in bestimmten
harmonischen Rhythmus zu Nachbar-Farben steht. Die Frequenz ist hier C-G-G´
oder C-C´ im Sinne der 12-Ton-Musik. Dies ergibt die Längenverhältnisse von
(-) zu (+) z.B.
< < < 3^-4 ; 3^-3 ; 3^-2 ; 3^-1 ; 3^0 ; 3^1 ; 3^2 ; 3^3 ; 3^4 > > >
Diese Abstandsverhältnisse werden anschließend
als Metrik bezeichnet. Der Grund für die Einführung des Begriffes Metrik ist
der, dass zu den Abständen innerhalb der gleichen Metrik gleiche Bedingungen
der Stablängen in der Art herrschen, dass in jeder Distanz der Metrik ein
durch V=c bedingter Status-Wechsel die gleiche Wirkung wie die
Original-Raum-Zelle hat. D.h. wenn bei Rot in der Distanz x der Status zu
Grün geworden ist, dann haben auch alle Nachbar-Farben entsprechend geändert. Somit kann
logisch so determiniert werden, als wenn es eine Gleichzeitigkeit dort gäbe.
Jede Metrik hat ein bestimmtes Längenverhältnis zu der Nachbar-Metrik in
Richtung Groß und Klein. Die Längen entsprechen ʎ=c/F, Puls=hc/ʎ und h=
Puls▪ʎ/c .
Auf dem Denk-Weg zur Erklärung von Partikel und ihrer kaskadenförmig
angeordneten Felder verschiedener Metriken muss ein Blick auf die Geometrie
der Matrix geworfen werden.
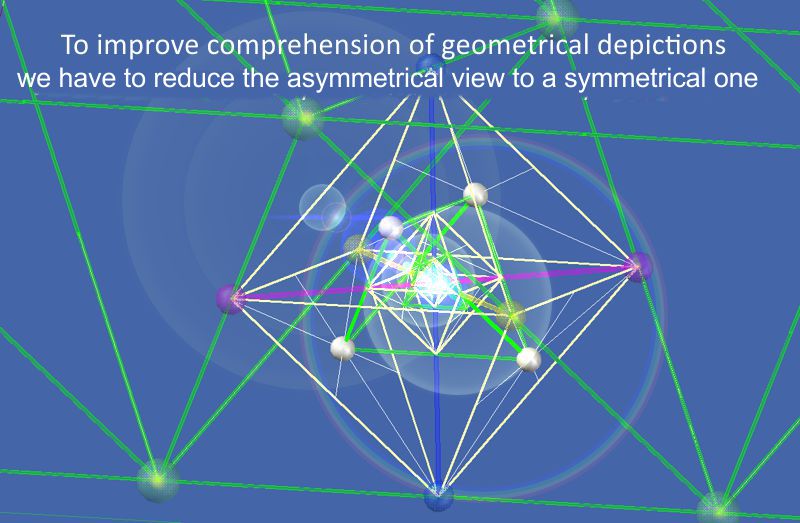
Hier wird klar, dass mit asymmetrischen Isometrien Bildern nur schwer die geometrischen Gesetze ablesbar werden. Die Darstellung sollte eine symmetrische Isometrie aufzeigen.
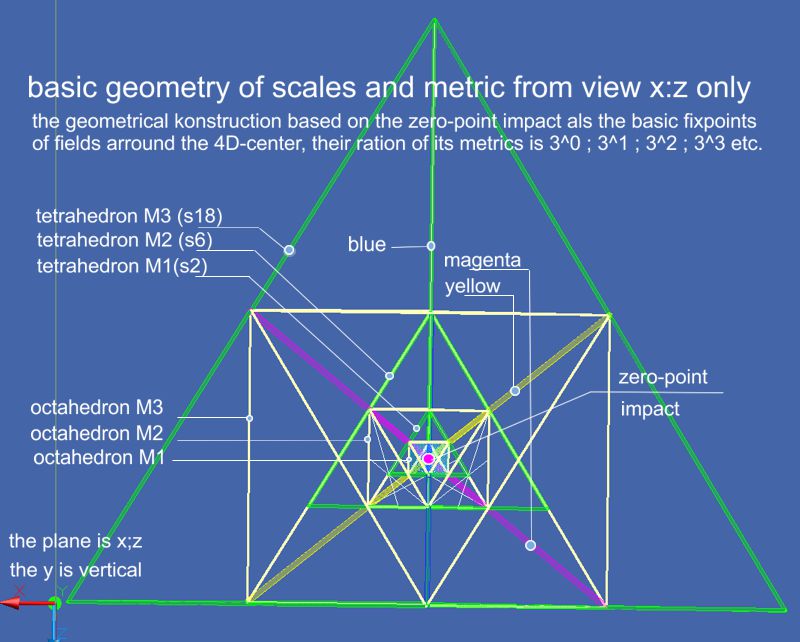
Das 2. Bild zeigt in Weiß die Oktaeder, in Grün die Tetraeder aus der Koordinatenstellung x;z, y als Senkrechte. Das Zentrum in den geometrischen Körpern ist exakt im gleichen Raum-Punkt. Während die geometrisch gleichen Formen verschachtelt sind, werden die Oktaeder einer Metrik von den Tetraedern der kleineren Metrik berührt. Gut sichtbar sind die 3 Diagonalen der Oktaeder mit ihren Farben, hier Magenta-Gelb-Blau, die unversetzt und in jeder Metrik weiterführend in die nächste höhere Metrik durch den Raum laufen. Dabei wird erkannt, dass alle Tetraeder die 4. Farbe, hier Grün haben. Dies gilt nur, wenn die Tetraeder jeweils die maximale Ausdehnung der metrischen Einheit wie S2; S4; S6 usw. repräsentieren. Das ist eine wichtige Erkenntnis: Während das weiße Oktaeder eine stehende Welle darstellt, ist das grüne Tetraeder der pulsübertragende Raum.
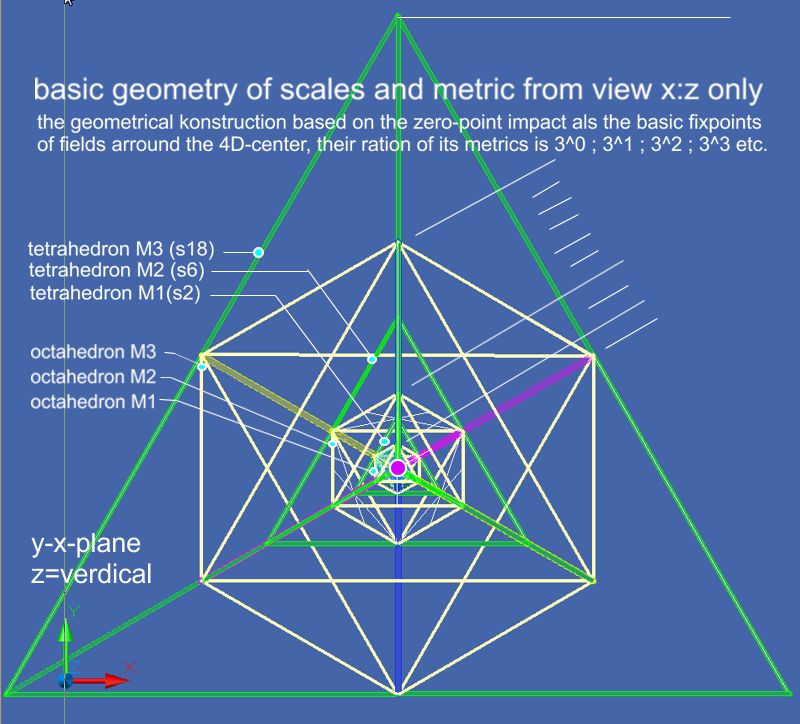
Das 3. Bild zeigt die Raumeinheit und ihre Metrik aus y;x mit z als vertikale Koordinate. Aus diesem Winkel erscheinen die Oktaeder als Hexagone und sind symmetrisch verschachtelt.
Wie kommt es zu der Vorstellung von Wellen?
Wie im Kapitel Oszillation beschrieben, kann sich der 3D-Raum als Fläche vorgestellt werden mit einer Vertikalen als Koordinate zum 4D-Raum. Bei den Koordinaten x;y;z wird z unterdrückt und mit n als Vektor zum 4D-Raum ersetzt. Da nun der 3D-Raum eine Raumstruktur ist, kann man sich aus praktischen Gründen die Fläche als einen dünnen Stoff vorstellen, dessen Netzwerk wie ein gestrickter Stoff mit Maschen der Fäden auch teilweise in die z-Richtung (bzw. hier n) vorstellen. Jede Masche ist hier ein Tetraeder mit 4 Eckpunkten (4 Farben).
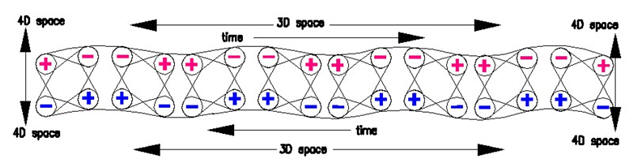
Damit wird die symbolische Fläche des Raumes z.T. real. Sie bekommt eine Ober- und Unterseite. In unserem Denkmodell kann unter bestimmten Umständen diese Fläche Biegungen in Form von Wellen bekommen. In diesem Sinne haben die Biegungen eine Oberseite, wo die Wellenspitze eine Zug-Spannung erzeugt und gleichzeitig eine Unterseite, wo diese Biegung eine Druckspannung erzeugt. Genau das aber passiert in der Realität. Die Phänomene auf der Oberseite erzeugen die Gegenwerte auf der Unterseite, ein Szenarium der Supersymmetrie wird gezeigt.
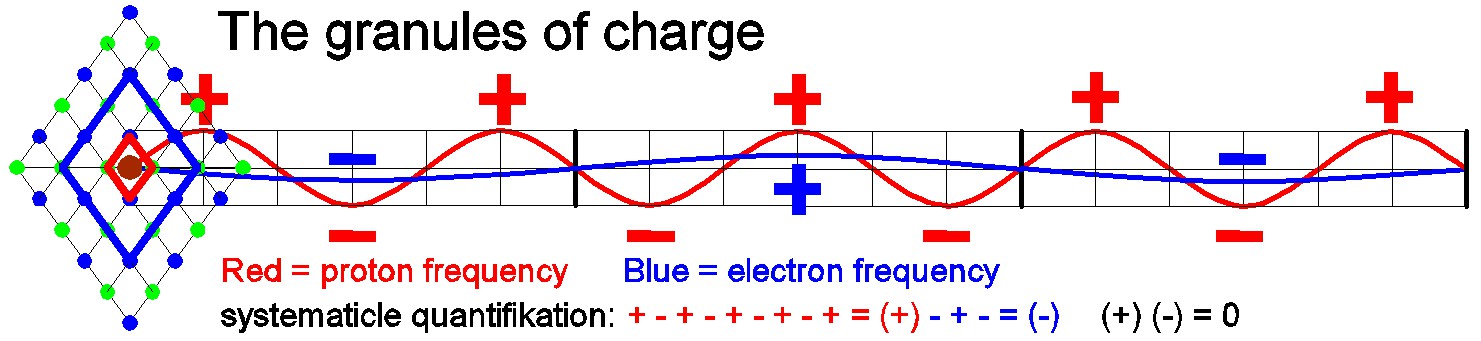
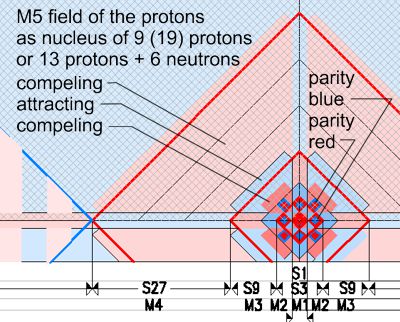
Das Bild zeigt auf der linken Seite die Raum-Größe M1 und M2 mit den Paritäten (+) und (-). In diesem Beispiel ist hier ein Proton in einem Positron, d.h. ein Neutron dargestellt. Es symbolisiert das Verhältnis der Biegungen (Wellen): Blau als M2 (S3) und Rot als M1 (S1) im Verhältnis 3 zu 1.
Raum bekommt Eigenschaften und diese bekommen Raum
Mit der Annahme einer 4. Raumdimension werden dem 3D-Raum Eigenschaften gegeben, die ohne sie nur als willkürliche Attribute den Partikeln und Feldern zugeordnet werden können. Hier werden sie jedoch erklärbar. Die 4. Raumdimension erwirkt eine punktuelle lokale Einwirkung auf den Raum. Lokale (oft als stehende) Felder können so erklärt werden, auch wenn das Medium des Raumes normaler Weise jede Einwirkung mit V=c fort tragen würde. Das erste Feld (M1) im 3D-Raum ist daher ein Sekundär-Feld und wird indirekt nur durch den 3D-Raum erzeugt. Die Planck-Konstante im 4D-Raum kann gleich oder anders sein, sie hat keinen direkten Einfluss im 3D-Raum.
Kulminierung (ein Erklärungs-Versuch, der sich als falsch erwies)
Das erste Feld M1 hat somit seine eigene Zeit und Frequenz, die jedoch der Frequenz des 4D-Impulses entsprechen muss, auch wenn der Impuls dieser Frequenz nicht entspricht. Theoretisch hat ein Impakt mit einem Vektor von 4D keinen direkten Einfluss, seine Frequenz jedoch schon. Damit kommt es unweigerlich zu einer Aufstapelung von Wirkungs-Quanten in ähnlicher Form wie im Kapitel „Die Dynamik der Matrix“ angedeutet wurde.
Die Felder um den 4D-Impuls im 3D-Raum werden daher von 2 Ursachen generiert.
1. Von der QT-Dynamik, ausgehend von der Frequenz des 4D-Impaktes.
2. Von der Aufstapelung
durch die höheren Frequenz des
M1 in den folgenden Räumen.
Punkt 1 erzeugt eine Feldhierarchie harmonisch abgestufter Amplituden.
Punkt 2 erzeugt eine multiple Welle, die sich von M1 zu M2 zu M3 usw.
ergiesst, bis eine Entropie bzw. Gleichheit mit den umgebenden Feldern
ergibt.
Diese beiden Feld-Generierungen kulminieren und ergeben die Hierarchie oder
Konstellation der Felder eines Partikels. Trotz des Punktes 2 können die
Feldverhältnisse der einzelnen Partikel ohne die Aufstapelung verglichen
werden, da diese nur auf die Amplitude der Felder bzw. ihrer Dichte einen
Einfluss hat, die Paritäten dieser Felder jedoch nicht beeinflusst.
Hier liegt ein großer Denkfehler versteckt!!!
In der QT kann es keine Kulminierung geben. Jede Änderung der Frequenz hat eine spontane Änderung des Feldradius zur Folge, was eine Kulminierung der Amplituden sofort ausgleicht. Ein stabiles Teilchen wie das Proton kann keine Kulminierung haben. Es ist immer eine harmonische Feld-Hierarchie, die von h=Puls ▪ F/c gebildet wird. Diese spezielle Hierarchie der Felder um das Teilchen entspricht der geometrischen Konstellation der Matrix als lokales Ergebnis eines 4D-Impaktes. Dort führt ein Höhepunkt der Feldamplituden zu einer spontanen Biegung des Hyperraums (4D). Jede Kulmination von Feldern in dieser Grössenordnung ist nur mit hoher Energie und nur an bestimmten geometrischen Stellen möglich. Auch das durch den 4D-Impakt verursachte M1-Feld wird vollständig von der Regel h=Impuls ▪ F/c beherrscht.
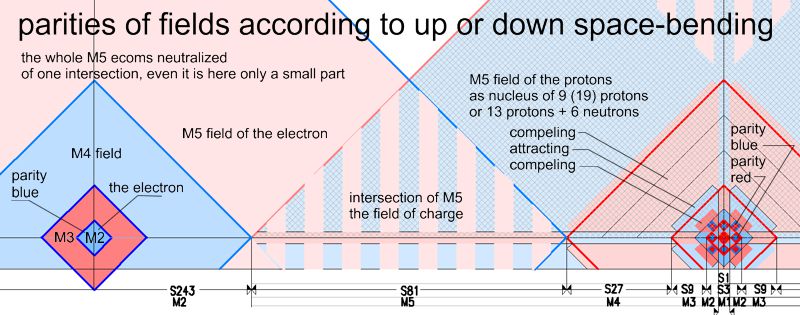
Das Bild zeigt die Beeinflussung der Feld-Paritäten eines Atomkerns (Atomgewicht 19) und eines Elektrons auf dem S-Orbit bzw. K-Schale. Anstatt Ladung wird hier der Ausdruck Parität benutzt. Das hat Sinn, da es ja, wie in Matrix-Ladung beschrieben, das Verbiegen des 3D-Raumes ist, was den Effekt der Anziehung / Abstoßung verursacht. Diese Verbiegung ist jedoch nicht statisch sondern oszilliert. Ein glatter Raum kann nicht oszillieren, eine Verbiegung hingegen erfordert eine Oszillation. Die Oszillation hingegen kann keine Ladung haben. Sie ist (+) und (-). Da alle Raumabstände harmonisch korrelieren und mit eigener Metrik eine eigene Zeit und Puls haben, sind harmonisch gestaffelte Oszillationen möglich. D.h. wenn zwei Felder die gleiche Parität (++) oder (--) haben, dann stoßen sie sich ab, wenn sie eine andere Parität haben (+-) oder (-+), dann ziehen sie sich an. Mit der Hierarchie der Raum- oder Feld-Größen und ihrer eigenen Metrik wurde auch das Problem der V=c gelöst, da die Hierarchien der harmonisch verschachtelten Raum-Größen eine Interaktion von syncroner oder assyncroner Oszilation (je nach Parität) haben und somit zeit-unabhängig sind. Das heisst, bei grosser Distanz wirken die grossen Felder (M9; M10 usw.), bei kleiner Distanz die kleinen Felder (M2;M3 usw.). Zeit existiert hier nur für Objekte ausserhalb der Oszillation.
Was genau bedeutet das?
Alle Interaktionen passieren so, als wenn sie zeitgleich sind. Durch die
eigene Metrik der Raum-Größen M1; M2; M3; usw. gibt es kein Zeit-Effekt
mehr, nur noch Paritäten. Wenn z.B. ein Partikel P1 (x1;y1;z1)
 mit Partikel
P2 (x2;y2;z2) interagiert, P1 die Parität + und P2 die Parität – hat, dann
ist es egal, wo sich ihre Felder schneiten. P1 kann mit dem eigenen M3 Feld
nur mit dem M3 von P2 interagieren. Die Felder, unabhängig wo, interagieren
immer mit (+-) oder (-+) und werden in diesem Fall angezogen. Dabei ändern
sie ihre Werte in Pica Sekunden von (+-) zu (-+), ihre Parität ändert immer
mit dem Ort, sie werden immer angezogen, egal welchen Oszillations-Status
sie haben. Interagieren bedeutet immer eine Feldüberlagerung der gleichen
Feld-Größe z.B. P1 mit M4 und P2 mit M4. Nochmal in Klartext: Der Rhythmus
der Oszillation dieser Feldart (hier das Ladungsfeld) ist im ganzen Universum gleich.
Obwohl die Zeitverzögerung
V=c mit eingebaut ist, hat sie keinen Einfluss auf die Beziehung des
Feld-Status, da ja
eine Teilchenoszillation NICHT wandert, sondern propagiert und immer ein
Geschehnis des Ortes ist. Damit ist die angebundenen Eigenschaften wie
Ladung von V=c unabhängig und wirkt als dauernde Wirkung.
mit Partikel
P2 (x2;y2;z2) interagiert, P1 die Parität + und P2 die Parität – hat, dann
ist es egal, wo sich ihre Felder schneiten. P1 kann mit dem eigenen M3 Feld
nur mit dem M3 von P2 interagieren. Die Felder, unabhängig wo, interagieren
immer mit (+-) oder (-+) und werden in diesem Fall angezogen. Dabei ändern
sie ihre Werte in Pica Sekunden von (+-) zu (-+), ihre Parität ändert immer
mit dem Ort, sie werden immer angezogen, egal welchen Oszillations-Status
sie haben. Interagieren bedeutet immer eine Feldüberlagerung der gleichen
Feld-Größe z.B. P1 mit M4 und P2 mit M4. Nochmal in Klartext: Der Rhythmus
der Oszillation dieser Feldart (hier das Ladungsfeld) ist im ganzen Universum gleich.
Obwohl die Zeitverzögerung
V=c mit eingebaut ist, hat sie keinen Einfluss auf die Beziehung des
Feld-Status, da ja
eine Teilchenoszillation NICHT wandert, sondern propagiert und immer ein
Geschehnis des Ortes ist. Damit ist die angebundenen Eigenschaften wie
Ladung von V=c unabhängig und wirkt als dauernde Wirkung.
Felder des Protons
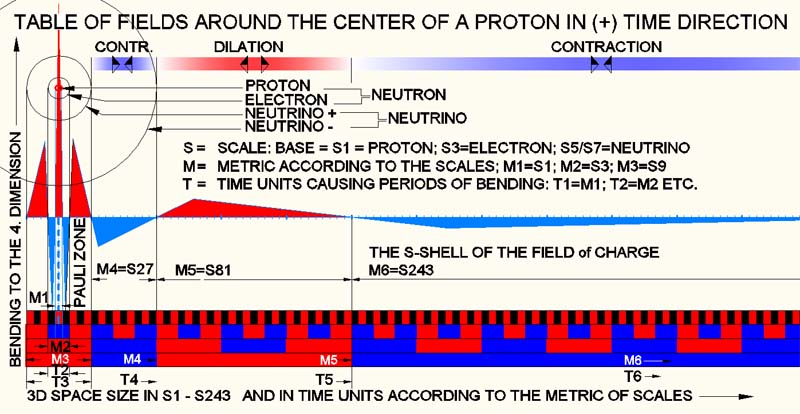
Die Verbiegung des 3D-Raumes passiert zuerst in M1. M1 korreliert entweder
mit der vom 4D Impakt (der 4D-Oszillation) entsprechenden Frequenz (F=h/p)
oder diese braucht noch M2, M3, M4 usw. bis der Quanten-Stapel
abgebaut ist und die Frequenz der Oszillation der Metrik entspricht. Kurz:
Es bildet sich ein Gleichgewicht (schon bei der Geburt
des Universums oder bei der Entstehung des Protons). Danach fließt keine
Energie. Jede Asymmetrie hätte sich ja bei der Geburt des Universums schon
aufgelöst. Überlebt hätte nur ein vollkommenes System, dessen Werte die
Summe Null ergeben. Im Falle eines Protons bedeutet dies (lt. Experimenten)
eine Lebenszeit von 10^27 Jahren, also länger als das Alter des Universums?!?
Die Raumgrößen M1; M2: M3 usw. sind im Prinzip leere Quanten, die
„straffrei“ aufgefüllt werden können ohne einen Fluss der Energien zu
verursachen. Das Bild oben zeigt die Kaskaden der metrischen Felder um ein
Proton. Diese Felder sind nicht nur Wirkungsfelder im 3D-Bereich, sondern
auch Verbiegungen (wie schematisch mit den Dreiecken angedeutet) aus der
4D-Sicht. Wie im Link in der Matrix beschrieben:
Oszillation
, bewirkt die Verbiegung Kompressions- und Dekompressions-Bereiche im
3D-Raum. Es ist die Elastizität der Matrix als Medium, die in den
Kombinationen solcher Bereiche den Ausgleich sucht, was die Wirkung
Anziehung oder Abstoßung
anstelle von Ladungswerten (+) und (-) bewirkt.
Damit wird nun die (elektrische) Ladung als innerer Wer im Quantenbereich
erklärt anstatt willkürlich aus rein mathematischen Gründen festgelegt.
Felder des Elektrons
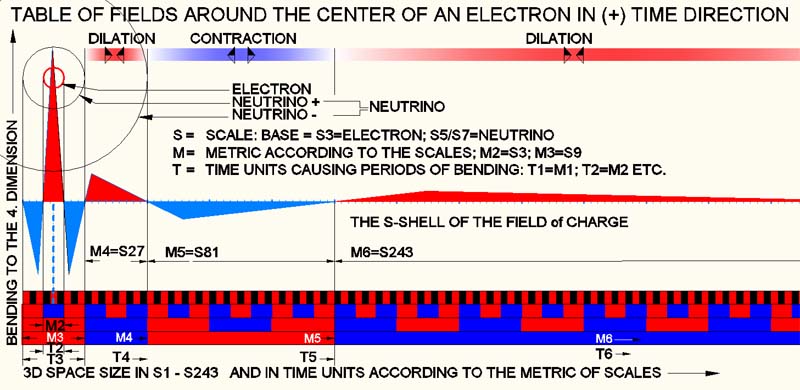
Das obere Bild zeigt die schematische Feld-Darstellung eines Elektrons. Auf den ersten Blick ist kaum ein Unterschied der Feldaufteilung zu der des Protons zu erkennen. Das kommt daher, dass die Metrik aller Felder gleich ist, nur der Einsatz-Impuls aus dem 4D-Raum ist unterschiedlich. Das Elektron hat seinen Impuls in M2 anstatt M1 wie das Proton. Dadurch, dass M2 dem Zeit-Puls T2 entspricht, ist die Biegung des 3D-Raumes an dieser Stelle gegenläufig (Kontra-Parität) , der Moment fließt gegenläufig in M3. Das setzt sich in allen Feldern fort, da alle Felder der Matrix eine gleiche Metrik für alle Impulse hat.
Die Parität der Felder
Nun bahnt sich ein neues Szenarium an: Die in Wirklichkeit kugelförmig um
den 4D-Impuls (eine Punkt-Größe) angeordneten Felder (oder vorsichtig
ausgedrückt: Bereiche), haben Paritäten in Form bestimmter mit der Metrik
korrelierender Frequenzen, da der 4D-Impuls eigentlich eine Oszillation ist.
Trotzdem können diese Frequenzen außer Acht gelassen werden, da sie in sich
selber kompatibel sind, d.h. einem (+) Feld immer mit (+) anfängt und
aufhört, selbst wenn das Feld viel grösser ist. Dieser Effekt wurde mit dem
unteren Balken Schwarz-Rot
bzw. Blau-
Rot
gekennzeichnet. Es soll immer daran erinnert werden, dass ja der Matrix-Raum
aus kleinen Zyklen von 4 Farben als
Doppel-Oszillation besteht, die geometrisch als Tetraeder
die Struktur des Raumes bilden.
Oszillation
Es können daher nicht beliebige
Konstellationen gelten, sie alle müssen nach dem Gesetz der MATRX geschehen,
da sie ja aus dieser existieren.
Die obigen Bilder zeigen im Vergleich
gleich große Bereiche verschiedener Parität. Kulminieren die Bereiche zB.
Bereich der Ladung, dann resultieren sie in Null, was in der Realität eine
Glättung des 3 dimensionalen Raumes bedeutet. Diese Glättung des Raumes
hingegen ist die Entlastung der Raum-Elastizität, die Spannung in diesem
Bereich löst sich. Dies bewirkt den Effekt der Anziehung, bestehend aus der
Tendenz, den Raum zu entlasten. Der wichtigste dieser hier im Bild
dargestellten Bereiche ist der Ladungs-Bereich. Alle Bereiche sind getrennt
von Bereichen mit Kontra-Parität, die in diesem Falle hier als Abstoßung
wirken. Diese garantieren die Stabilität solcher Konstellationen. Der
Ladungsbereich wird in der Physik als EM-Raum angesehen, da man dort noch
nicht soweit ist, die Geschehnisse dieses Bereiches als lokal in Raum
UND Zeit anzusehen und
die Meinung hat, dass ein Elektron, ein Proton oder anderes Teilchen etwas
Separates vom Raum ist. Hier ist es jedoch nur ein Zustand des Raumes bzw.
der Matrix.
Die Felder des Neutrons
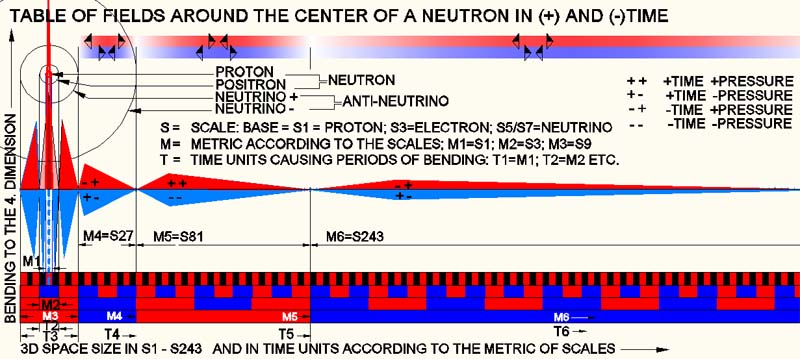
Das obige Bild zeigt die Felder eines Neutrons. Nach heutiger Physik zerfällt ein Neutron beim Beta-Zerfall in ein Proton, ein Positron und ein Antineutrino. Ich nahm aus diesem Grunde ein Proton und ein Anti-Elektron (hier Positron) in die Paritäten-Feld-Tabelle auf, um zu sehen was daraus wird. Ich probierte es tatsächlich zuerst mit einem Proton und einem Elektron. Dies ergab jedoch nur eine Kulminierung der Feld-Amplituden. Ich suchte jedoch, die sich ergänzende Wirkung der Felder zu finden. Das Antielektron kulminierte mit M1 und M2 in dem Maße, dass der Kompressionsteil des Protons in M1 mit dem M2-Teil des Antielektrons kulminiert wurde, der Teil in M2 sich jedoch vom M2-Teil des Protons weitgehend egalisiert wurde. Die Kulminierung hatte dadurch nur eine minime Wirkung. Alle anderen Felder jedoch glichen sich aus und konnten dem 3D-Raum keine Werte übergeben. Das Neutron wurde deshalb minim „schwerer“, hatte sonst jedoch keinen Einfluss auf den Raum (elektrisch neutral).
Nun ein Wort zur Darstellung:
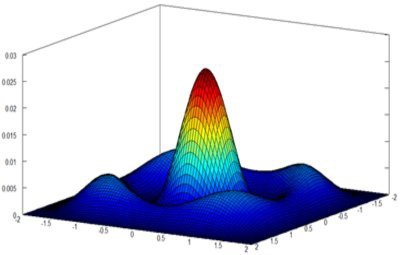 Nebenstehendes
Bild zeigt den Raum als x.y und den Energiewert als z. Die Farben haben
keine Extra-Aussage, sie unterstreichen nur die z-Werte. Mit dieser
aufwendigen Graphik kann nur sehr wenig dargestellt werden. Es könnte
Teilaspekte eines Partikels darstellen, nicht aber das Anti-Partikel oder
seine Ladung. Es können keine Zusammenhänge zu Quanten-Bereiche gleicher
Größe (Metrik) und keine Paritäten dargestellt werden. Die Theorie bleibt
weiterhin eine nicht darstellbare Theorie. Die obere Darstellung (Table of
fields) versucht graphisch, Zusammenhänge zu erfassen, die bis dahin von der
QM nicht gemacht wurden. Die besten Darstellungen in QM sind die
Feynman-Graphs, die jedoch in dieser Weise nur die theoretischen Resultate
darstellt, umgekehrt aber keine solche Resultate beweisen.
Nebenstehendes
Bild zeigt den Raum als x.y und den Energiewert als z. Die Farben haben
keine Extra-Aussage, sie unterstreichen nur die z-Werte. Mit dieser
aufwendigen Graphik kann nur sehr wenig dargestellt werden. Es könnte
Teilaspekte eines Partikels darstellen, nicht aber das Anti-Partikel oder
seine Ladung. Es können keine Zusammenhänge zu Quanten-Bereiche gleicher
Größe (Metrik) und keine Paritäten dargestellt werden. Die Theorie bleibt
weiterhin eine nicht darstellbare Theorie. Die obere Darstellung (Table of
fields) versucht graphisch, Zusammenhänge zu erfassen, die bis dahin von der
QM nicht gemacht wurden. Die besten Darstellungen in QM sind die
Feynman-Graphs, die jedoch in dieser Weise nur die theoretischen Resultate
darstellt, umgekehrt aber keine solche Resultate beweisen.
Partikelphysik als LHC Erzeugnis (LHC = Large Hadron Collider)
Die Entdeckung der Elektronen, Protonen, Neutronen, Neutrinos und ihre Antiteile hatte eine lange Geschichte. Die Entdeckung Ihrer Trümmer im Schutt der Nebelkammern in LHC erbrachte in ihrer kurzen Geschichte eine reiche Ausbeute von Teilchen aller Art. In der Matrix-Theorie sind sie in direkter Weise nicht nachweisbar. Unabhängig von dem Ausdruck Partikel – Feld – Oszillation steht fest, dass die obengenannten Teilchen stabil sind und eine Lebenszeit von vielen Jahren haben (Proton = 10^27 Jahren) Ihre Trümmer jedoch haben eine kurze Lebenszeit von ca 10^-20 (0.00000….) Jahren und in der Nebelkammer nur eine Spur von Ångström. Es stellt sich nun die Frage, ob diese Funken bei den brutalen Hochenergie-Versuchen Teilchen genannt werden können. Hier muss in Betracht gezogen werden, dass die Matrix-Struktur in Raum-Zeit-Puls als geometrische Struktur Trümmer ebenfalls nur mit geometrischen Quanten-Werten erbringt. Chaotische und willkürliche Werte sind hier nicht möglich. Kein Wunder, dass die Ruhm-behaftete Namensgebung zu einer Großzahl von Partikel geführt hat. Die hier dargestellte Theorie löst alles in Paritäten auf, wobei Anziehung und Abstoßung eine Parität der Beugung des 3D-Raumes in die 4D-Koordinate ist.
Für ein tieferes Verständnis zur Matrix-Theorie empfehle ich meine weiteren Schriften.
die Matrix des Weltmediums
Die Schwingung des Welt-Mediums
die Geometrie des Mediums Raum
Das Universum
Friedmann-space and the space-matrix
Das Raum-Zeit-Kontinuum
Die Raum-Zeit-Illusion
Teilchen in der Matrix Struktur
Das Elektron
Gunter Michaelis, Lützelflüh, 20.12.2020 Switzerland
